【E資格】機械学習レポート

この度E資格を受ける前 E資格を受けるために現在ラビットチャレンジを受講中である。その受講内容をレポートとしてまとめる。

今回は機械学習について学んだこと・気づいたことを記す。

機械学習とは

トム・ミッチェルによると機械学習では機械に認識の仕方ではなくて学習の仕方をプログラムしている。つまり、機械学習のコンピュータプログラムはアプリケーションにさせたいこと（タスクT）を性能指標Pで測定してその性能がデータによる経験により改善される場合、タスクTおよび性能指標Pに関して経験Eから学習するとしている。

線形回帰モデル

概要

• 線形回帰モデルはある入力値から直線的に出力を予測するモデル
  $$ \hat\y = w_0 + w_1x_1 + w_2x_2 + \varepsilon $$
• 教師データ（説明変数と目的変数）が存在
• 予測値の算出方法：$$ y = w^Tx + _0 = \sum_j=1^mw_jx_j + w_0 (パラメータwは未知)$$
• 線形回帰モデルの弱点として下記が挙げられる
  1. 外れ値が全体に大きく影響を与えること
  2. 説明変数間で相関性が高いと重複してデータ容量が無駄に大きくなること
• 線形回帰モデルでは最小二乗誤差(MSE; Mean Squared Error)を最小とするパラメータの推定を目的としている
  $$　MSE=1/n\sum(y-\hat\y)\ $$

実装（単回帰分析）

boston_loadというデータセットを使って米ボストンの住宅価格に影響する説明変数を推定する。

#load_bostonをインポート
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np

boston = load_boston()

変数の一覧を見るコードは下記の通り

#load_bostonの説明変数の一覧を抽出
print(boston["DESCR"])

抽出された説明変数の一部は下記の通り

記号名	説明変数
CRIM	犯罪発生率
RM	一戸当たりの平均部屋数
AGE	1940年よりも前に建てられた家屋の割合
DIS	ボストンの主な5つの雇用圏までの重み付き距離
PRICE	住宅価格の中央値（単位:$1,000）

load_boston内の変数を確認したら回帰分析で使用するデータフレームに組み合わせを確認するデータフレームを注入。データフレームが問題なくpythonコード上で取り組まれていることを確認する。

#　説明変数をDataFrameに変換
df = DataFrame(data=boston.data, columns = boston.feature_names)

# 目的変数からDataFrameに追加
df['PRICE'] = np.array(boston.target)

#DataFrameの最初の10行を表示
df.head(10)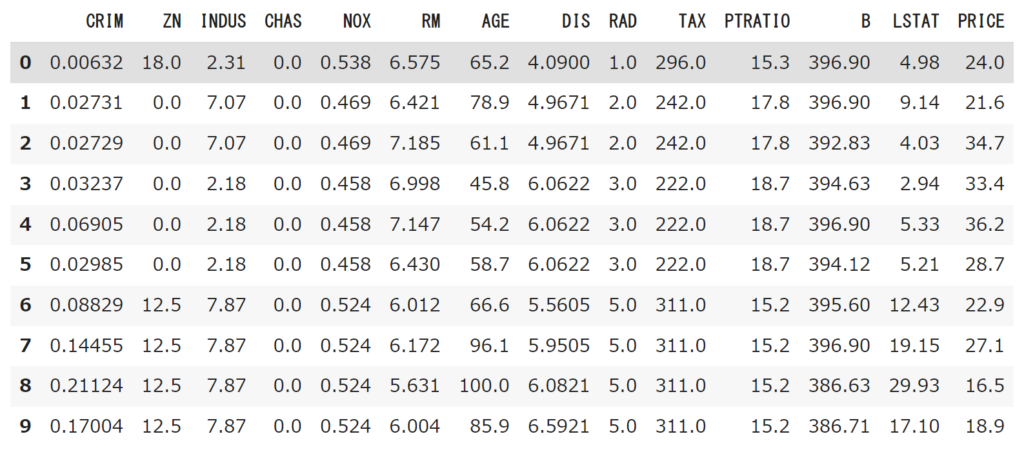

データの準備ができたらSkleaernでfit関数を用いてパラメータ推定を実施。今回は部屋数がボストンの住宅にどの程度影響が出るかを確認する。今回はボストンで一部屋の住宅を探した際の値段を推定した。
線形回帰をPythonで実装するときは作法としてモデル用のオブジェクトを実装することに留意する。

# 説明変数
data = df.loc[:, ['RM']].values

# 目的変数
target = df.loc[:, 'PRICE'].values

# sklearnLinearRegressionをインポート
from sklearn.linear_model import LinearRegression

# オブジェクト生成
model = LinearRegression()

# fit関数でパラメータ推定
model.fit(data, target)

#予測
model.predict([[1]])

上記の予測値はarray([-25.5685118])となり、ボストンで1部屋のところを購入すると約25,000ドル受け取れるという現実離れした推計になってしまった。

今回のボストンで1部屋の住宅を探した際の推計が現実離れしてしまった理由として外挿問題が考えられる。外挿問題とは、あるデータを使って訓練した機械学習モデルにおいて訓練モデルの範囲外で推定を行ってしまうという問題である。

つまり、load_bostonに1部屋の住宅のデータが入っていなければ訓練データ外で想定されていなかったタイプのモデルの出力値を推計することになり予測精度が低下する。今回住宅を借りたらお金がもらえるという非現実的な推計をしてしまったため、load_bostonの部屋数を確認する。

#データ内の部屋数を確認（サンプルとして10個）
df[['RM']].head(10)

その結果、load_bostonでは６，７部屋の住宅が多そうだということがサンプルから読み取れた。

したがって、6部屋ある住宅価格の推計を再度実施したところ、array([19.94203311])という値が算出され、正の値になったので妥当そうな推計だとデータを見出すことができた。

実装（重回帰分析）

単回帰分析では説明変数が1つであったのに対して、重回帰分析は説明変数を複数持つ回帰分析である。単回帰分析に引き続きボストン住宅の価格への影響で重回帰分析を実施する。説明変数にはAGE(1940年よりも前に建てられた家屋の割合)とDIS(ボストンの主な5つの雇用圏までの重み付き距離)を使用する。

AGE、DIS共に指標が上昇するとともに住宅価格が下がるという仮説を基に回帰分析を行う。まずはAGEとDISのデータを表示させ、推計時の適切な入力値を確認する。

#カラムを指定しデータ表示
df[['AGE','DIS']].head(10)

下記表よりAGEは50～100、DISは4～6が妥当な数値だと読み取った。

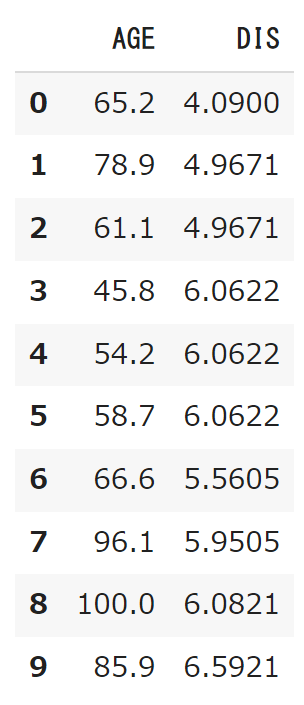
#説明変数
data2 = df.loc[:, ['AGE','DIS']].values

#目的変数
target2 = df.loc[:, 'PRICE'].values

#オブジェクト生成
model2 = LinearRegression()

#fit関数でパラメータ推定
model2.fit(data, target)

#予測(AGE_80, DIS_6)
model2.predict([[80,6]])

#予測(AGE_70, DIS_6)
model2.predict([[70,6]])

#予測(AGE_60, DIS_6)
model2.predict([[60,6]])

#予測(AGE_80, DIS_5)
model2.predict([[80,5]])

#予測(AGE_70, DIS_5)
model2.predict([[70,5]])

#予測(AGE_60, DIS_5)
model2.predict([[60,5]])

#予測(AGE_80, DIS_4)
model2.predict([[80,4]])

#予測(AGE_70, DIS_4)
model2.predict([[70,4]])

#予測(AGE_60, DIS_4)
model2.predict([[60,4]])

回帰分析した結果、下記のような結果となった。当初仮説通り、 AGE、DIS共に指標が上昇するとともに住宅価格が下がった。また、AGEの方が価格に与える影響が大きかった。

AGE/DIS	4	5	6
60	23.67603137	23.35898347	23.04193557
70	22.26702816	21.9499802	21.63293236
80	20.85802494	20.54097704	20.22392914

非線形回帰モデル

概要

• 複雑な非線形構造の現象に対して予測をする回帰モデル
  • あくまでも非線形な現象を回帰分析しているだけであり、モデル自体が非線形なわけではない（パラメータwに関しては線形な回帰モデル）
• 単回帰分析と同様に未知パラメータは最小二乗法や最尤法により推定
• 回帰関数として基底関数と呼ばれる既知の非線形関数とパラメータベクトルの非線形結合を使用
  $$ y = f(x_i) +\varepsilon_i $$
• より具体的には下記のような関数を使用
  • 多項式関数
  • ガウス型基底関数
  • スプライン関数/ Bスプライン関数
• 教師データ（説明変数と目的変数）が存在
  

未学習と過学習

• 未学習(Underfitting)
  • 意味：学習データに対して、十分小さな誤差が得られないモデル
    • 訓練誤差とテスト誤差の両方が大きい状態
  • 対策
    1. より表現力の高いモデルを利用
• 過学習(Overfitting)
  • 意味：訓練データでは精度の良い予測ができる（誤差が小さい）が、学習データに対して、十分小さな誤差が得られないモデル
    • 訓練誤差は小さいがテスト誤差が大きい場合
  • 対策
    1. 学習データ数の増加
    2. 不要な変数を削除して表現力を抑止（削除しなければならない組み合わせが多すぎて工数がかかる）
    3. 正則化による表現力を抑止

正則化

モデルが複雑になりすぎた際に、モデルの複雑さを抑止するために正則化項を設定する技法。正則化項を設定することでモデルの複雑性に対して罰則を与えるような役割を果たす。

$$ S_\gamma = (y – \phi_w)^T(y – \phi_w) + \gamma R(w) $$

正則化を使用する際は、上記関数が最小化されるように予測モデルに学習を促す。

そして 正則化には2つのアプローチが存在する。

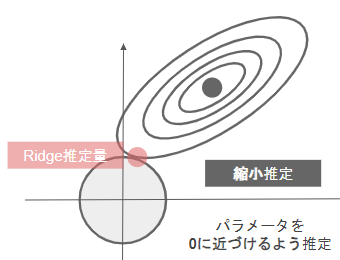
• Ridge回帰
  • 正則化項にL2ノルムを使用したもの
  • パラメータを0に近づけるするように推定するため縮小推定とも呼ばれる。Lasso回帰よりも過学習の抑止に長けている。

表記 $$ S_\gamma = (y – \phi_w)^T(y – \phi_w) + \gamma ||w||_1 $$

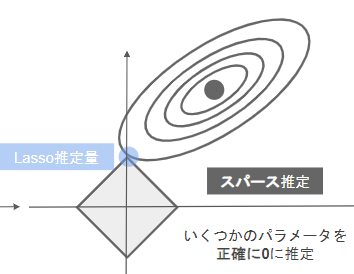
• Lasso回帰
  • 正則化項にL1ノルムを使用したもの
  • いくつかのパラメータを正確に0に推定するためスパース推定とも呼ばれる。Ridge回帰よりも不要なパラメータを削ることに長けている。

表記 $$ S_\gamma = (y – \phi_w)^T(y – \phi_w) + \gamma ||w||_2 $$

実装

非線形回帰モデルで分析した際の実装結果は下記の通り。

#必要モジュールをインポート
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

#seaborn設定
sns.set()
#背景変更
sns.set_style("darkgrid", {'grid.linestyle': '--'})
#大きさ(スケール変更)
sns.set_context("paper")

n=100

def true_func(x):
    z = 1-48*x+218*x**2-315*x**3+145*x**4
    return z 

def linear_func(x):
    z = x
    return z

data = np.random.rand(n).astype(np.float32)
data = np.sort(data)
target = true_func(data)

noise = 0.5 * np.random.randn(n) 
target = target  + noise
plt.scatter(data, target)

plt.title('NonLinear Regression')
plt.legend(loc=2)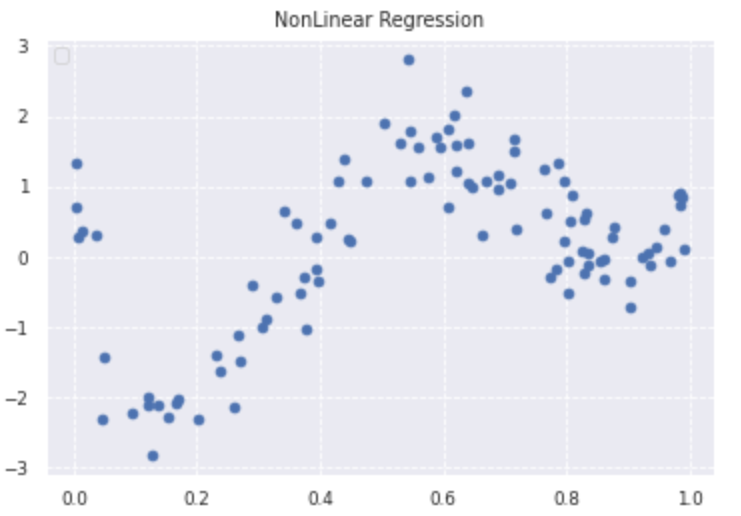

from sklearn.linear_model import LinearRegression

clf = LinearRegression()
data = data.reshape(-1,1)
target = target.reshape(-1,1)
clf.fit(data, target)
p_lin = clf.predict(data)

plt.scatter(data, target, label='data')
plt.plot(data, p_lin, color='green', marker='', linestyle='-', linewidth=1, markersize=3, label='Linear Regression')
plt.legend()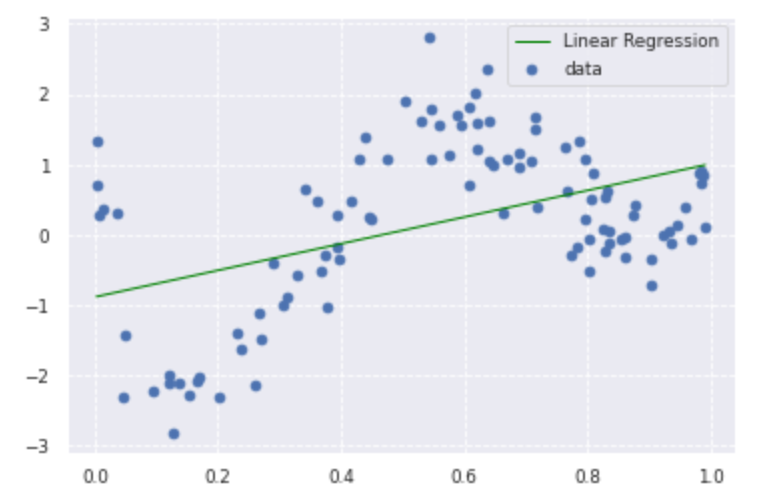

from sklearn.kernel_ridge import KernelRidge

clf = KernelRidge(alpha=0.0002, kernel='rbf')
clf.fit(data, target)

p_kridge = clf.predict(data)

plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend()

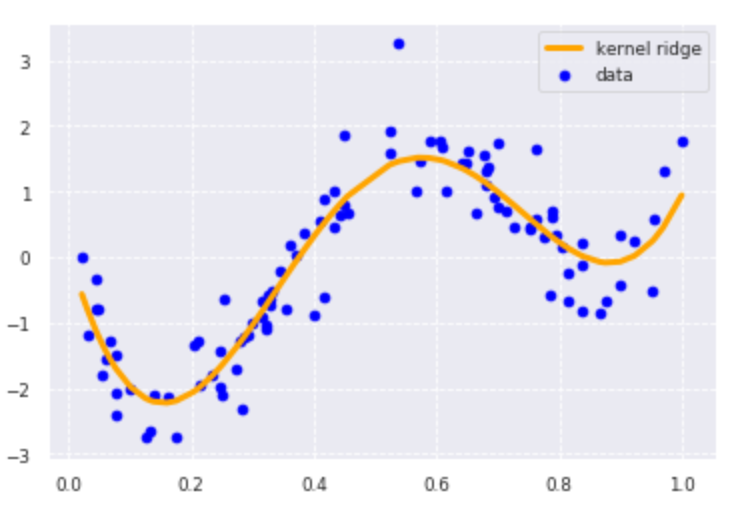
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge

kx = rbf_kernel(X=data, Y=data, gamma=50)

clf = Ridge(alpha=30)
clf.fit(kx, target)

p_ridge = clf.predict(kx)

plt.scatter(data, target,label='data')
for i in range(len(kx)):
    plt.plot(data, kx[i], color='black', linestyle='-', linewidth=1, markersize=3, label='rbf', alpha=0.2)

plt.plot(data, p_ridge, color='green', linestyle='-', linewidth=1, markersize=3,label='ridge regression')

print(clf.score(kx, target))

deg = [1,2,3,4,5,6,7,8,9,10]
for d in deg:
    regr = Pipeline([
        ('poly', PolynomialFeatures(degree=d)),
        ('linear', LinearRegression())
    ])
    regr.fit(data, target)
    p_poly = regr.predict(data)
    plt.scatter(data, target, label='data')
    plt.plot(data, p_poly, label='polynomial of degree %d' % (d))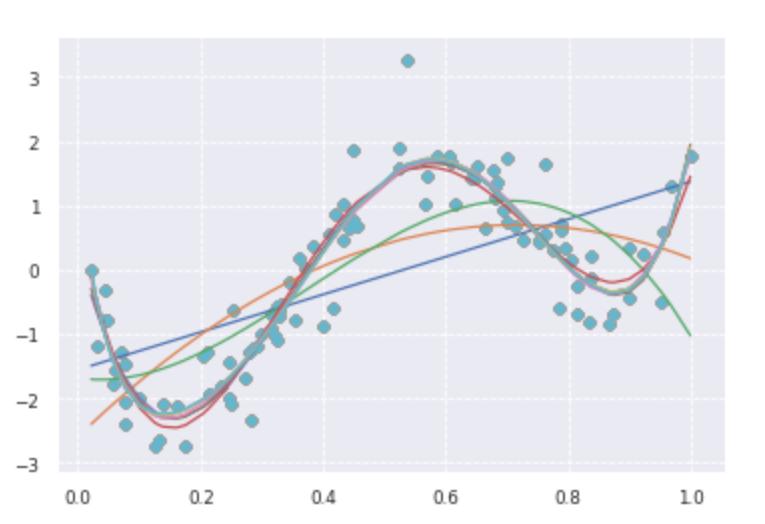

from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Lasso

kx = rbf_kernel(X=data, Y=data, gamma=5)

lasso_clf = Lasso(alpha=10000, max_iter=1000)
lasso_clf.fit(kx, target)

p_lasso = lasso_clf.predict(kx)

plt.scatter(data, target)

plt.plot(data, p_lasso, color='green', linestyle='-', linewidth=3, markersize=3)

print(lasso_clf.score(kx, target))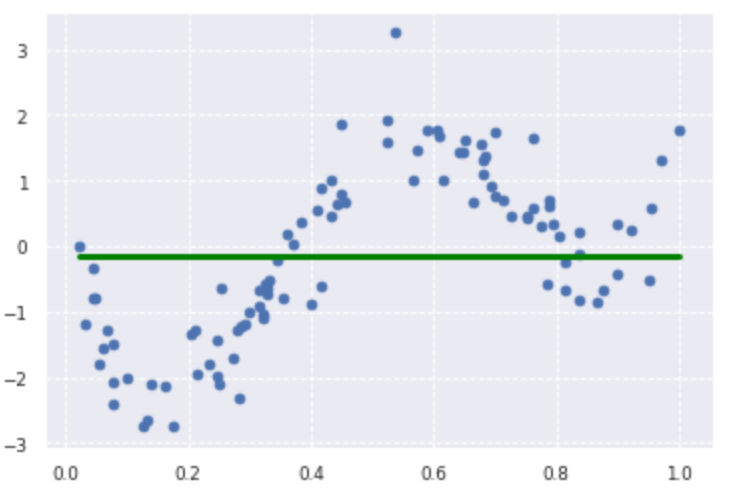

from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge

kx = rbf_kernel(X=data, Y=data, gamma=50)

clf = Ridge(alpha=30)
clf.fit(kx, target)

p_ridge = clf.predict(kx)

plt.scatter(data, target,label='data')
for i in range(len(kx)):
    plt.plot(data, kx[i], color='black', linestyle='-', linewidth=1, markersize=3, label='rbf', alpha=0.2)

plt.plot(data, p_ridge, color='green', linestyle='-', linewidth=1, markersize=3,label='ridge regression')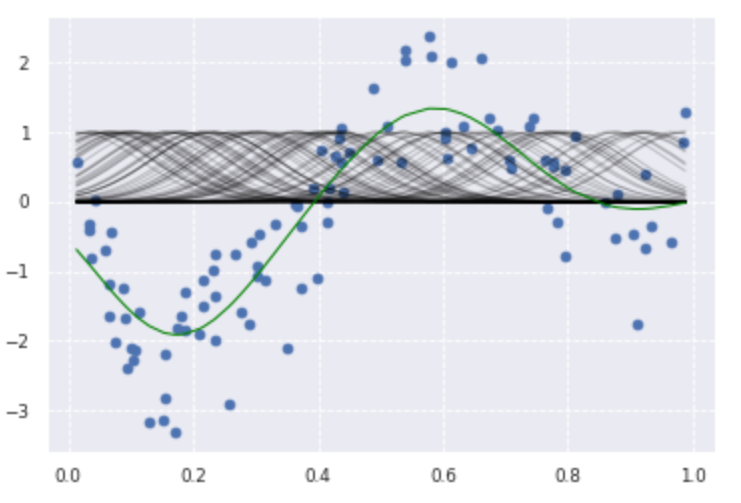

from sklearn import model_selection, preprocessing, linear_model, svm


clf_svr = svm.SVR(kernel='rbf', C=1e3, gamma=0.1, epsilon=0.1)
clf_svr.fit(data, target)
y_rbf = clf_svr.fit(data, target).predict(data)

plt.scatter(data, target, color='darkorange', label='data')
plt.plot(data, y_rbf, color='red', label='Support Vector Regression (RBF)')
plt.legend()
plt.show()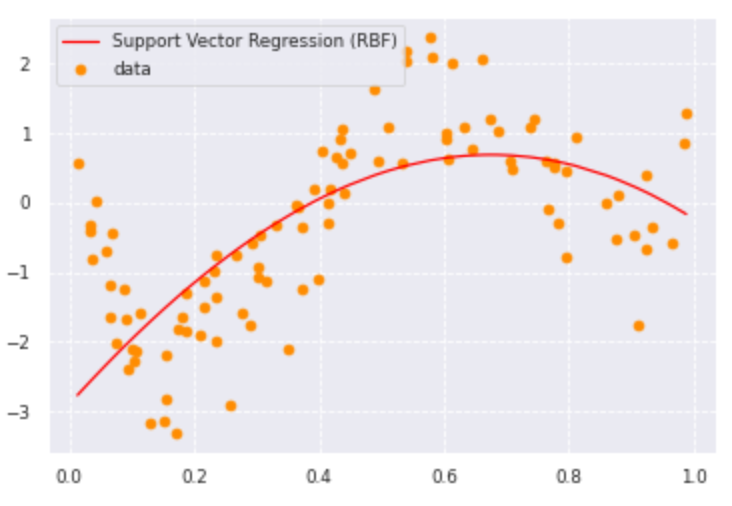

ロジスティック回帰モデル

概要

• 分類問題用の機械学習モデル
  $$ \hat\y = w^Tx+w_0 = \sum_{j-1}^m w_jx_j + w_0 $$
  • 入力（説明変数/特徴量）
    • m次元のベクトル（m=1の場合はスカラー係数）
  • 出力⇒0or1の値
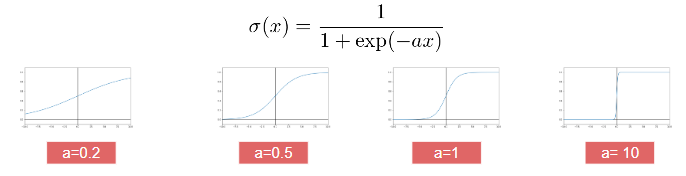
• シグモイド関数を利用しており出力はy=1のときなる確率の値になる
  • 実数の入力を0~1の範囲で出力

• 教師データ（説明変数と目的変数）が存在

最尤推定

ロジスティック回帰は教師ありの分類モデルとして利用される。出力時に活性化関数としてシグモイド関数を用いるため、出力を確率として解釈できる。

シグモイド関数は、全ての実数を定義域、(0,1)を値域とする関数である。
微分した形を自分自身だけで表せる。

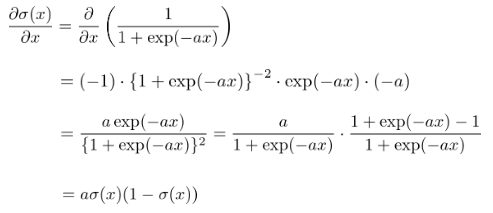
• ロジスティック回帰モデルでは確率の確度を示す関数（尤度関数L）を最大にするようなパラメータを推計

$$ P(y_1,y_2,…,y_n|w_1,w_2,…,w_n）= \Sigma_{i=1}^np_i^{y_i}(1-p_i)^{1-y_i}
=L(w)$$

• ロジスティック回帰の場合出力0以上1以下のため計算中のけた落ちを防ぐために対数を使用

$$ E(w_1,w_2,…,w_m）= -logL (w_1,w_2,…,w_m）= -\Sigma_{i=1}^n[y_ilogp_i + (1-y_i)log(1-p_i)] $$

尤度関数Lを最大化するためのアプローチとして勾配降下法が挙げられる。

• 勾配降下法（Gradient Descent；GD）
  • 反復学習によりパラメータを逐次的に更新するアプローチ
  • 学習率ηというハイポあーパラメータでモデルのパラメータの集約度合いを調整
  • ロジスティック回帰ではシグモイド関数を用いているためパラメータwを解析することが困難なためGDが必要となる

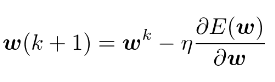
パラメータが更新された場合、勾配が0になっていることを示すので、反復学習で探索した範囲での最適解が算出されたことを意味する。

但し、勾配法ではパラメータを更新する際に李お湯しているすべてのデータに対する輪を求める必要があるため、メモリの要領の浪費や計算スピードが遅いといったデメリットが存在。

• 確率的勾配降下法（Stochastic Gradient Descent；SGD）
  • GDをベースとしてデータを一つずつランダムに選んでパラメータを更新する方法
  • 勾配降下法で1回パラメータを更新するときと同じ計算量でパラメータをn回更新できるため効率的に最適解を探索可能

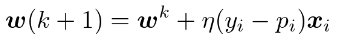
実装

タイタニックの乗客データに基づいて変数と生存結果の関連性を調査。
まずは運賃と生存結果については下記の通り。

import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

titanic_df = pd.read_csv('.../data/titanic_train.csv') #ファイルの格納場所のためマスキング
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())

data1 = titanic_df.loc[:, ["Fare"]].values
label1 =  titanic_df.loc[:,["Survived"]].values
model=LogisticRegression()
model.fit(data1, label1)

w_0 = model.intercept_[0]
w_1 = model.coef_[0,0]

def sigmoid(x):
    return 1 / (1+np.exp(-(w_1*x+w_0)))

x_range = np.linspace(-1, 500, 3000)

plt.figure(figsize=(9,5))
#plt.xkcd()
plt.legend(loc=2)

plt.plot(data1,np.zeros(len(data1)), 'o')
plt.plot(data1, model.predict_proba(data1), 'o')
plt.plot(x_range, sigmoid(x_range), '-')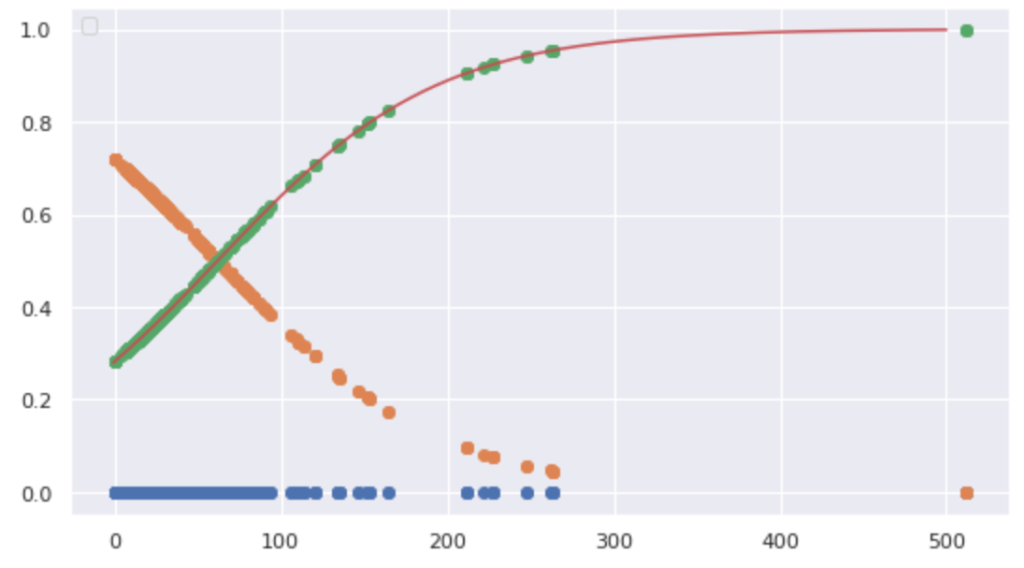

62ドルを境に生存率に変化が見られた。すなわち61ドル以下から死亡する確率が生存率を上回った。
また、タイタニック号における性別と階級の2つの変数と生存率の相関も分析した。

titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)
titanic_df = titanic_df.drop(['Pclass', 'Sex', 'Gender','Age'], axis=1)

np.random.seed = 0

xmin, xmax = -5, 85
ymin, ymax = 0.5, 4.5

index_survived = titanic_df[titanic_df["Survived"]==0].index
index_notsurvived = titanic_df[titanic_df["Survived"]==1].index

from matplotlib.colors import ListedColormap
fig, ax = plt.subplots()
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'],
                titanic_df.loc[index_survived, 'Pclass_Gender']+(np.random.rand(len(index_survived))-0.5)*0.1,
                color='r', label='Not Survived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'],
                titanic_df.loc[index_notsurvived, 'Pclass_Gender']+(np.random.rand(len(index_notsurvived))-0.5)*0.1,
                color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.legend(bbox_to_anchor=(1.4, 1.03))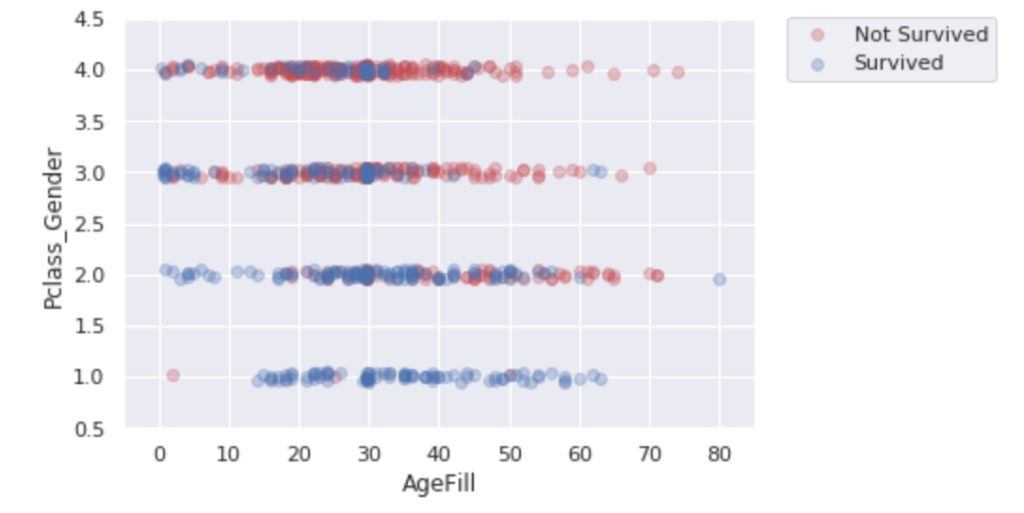

縦軸は性別（女性＝0、男性=1）と乗客の社会階級（High=1、Middle=2、Low=3）の合計値を示している。したがってグラフ上で上にプロットされている人ほど男性かつ社会階級が低い層がデータとして示される。

また、右上の凡例にある通り、赤色がNot Survived、青色がSurvivedであるため、縦軸で下の方に示されている人の方が生存している人が多い。したがって、階級の高い女性が生存数が多く、優先的に避難誘導されたと推察することができる。

主成分分析

概要

• 多変量のデータ構造をより指標がより少なく圧縮した分析手法（例：100次元⇒3次元）
  • 変量の個数を減らすことで失われる情報量を最小化するように設定する必要あり
  • 少数変数を利用した分析や可視化（2・3次元の場合）が可能

• 係数ベクトルが変われば線形変換後の値が変化
  • 分散の大きさを情報量と定義
  • 線形変形後の変数の分散が最大となる射影軸を探索

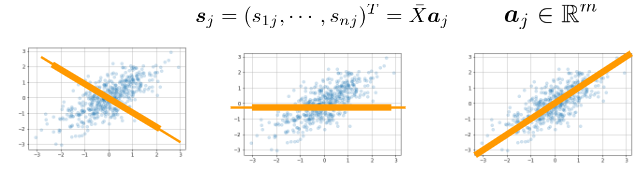
• 主成分分析を実施するにあたり下記のような制約を考慮する必要あり。

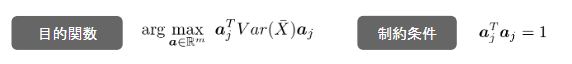
ラグランジュ関数

主成分分析ではラグランジェ関数の微分により最適解を算出

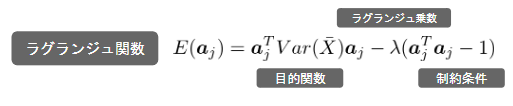
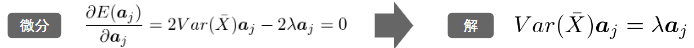
寄与率

• 主成分＝ある固有値（昇順）に対応する固有ベクトル
• 寄与率＝第k主成分の主成分が持つ情報量の割合
  • 分散の大きさを情報量として定義しているため、第~元時限分の主成分の分散は元データの分散と一致する
  • 第k主成分の分散は主成分に対応する固有値

• 累積寄与率＝第1~k主成分までに圧縮した際の情報損失量の割合

実装

与えられた乳がんデータを利用してデータの次元を圧縮する。初めに下記コードより与えられている乳がんデータは33次元であることがわかる。

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
%matplotlib inline

cancer_df = pd.read_csv('.../data/cancer.csv') #ファイルの格納場所のためマスキング
print('cancer df shape: {}'.format(cancer_df.shape))

>>>cancer df shape: (569, 33)

乳がんデータ主成分分析を実施し、寄与率を調べると第1主成分が約43％、第2主成分が約20%を占めていることが判明した。

cancer_df.drop('Unnamed: 32', axis=1, inplace=True)
cancer_df

y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)
X = cancer_df.loc[:, 'radius_mean':]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

pca = PCA(n_components=30)
pca.fit(X_train_scaled)
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)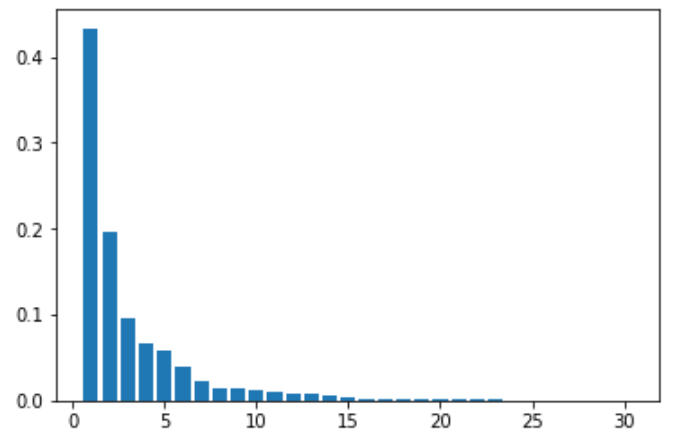

乳がんデータを主成分分析を利用し、33次元から2次元に圧縮した結果、良性と悪性の境界線が不明瞭になり情報量を落としすぎたことが見受けられる。
上記の寄与率の棒グラフを確認すれば、第3～6主成分も10%～5％弱の一定の情報量を占めており、何でもかんでも次元を圧縮すれば制度のいい分析ができるとは限らないことを学んだ。

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print('X_train_pca shape: {}'.format(X_train_pca.shape))
# X_train_pca shape: (426, 2)


print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))


temp = pd.DataFrame(X_train_pca)
temp['Outcome'] = y_train.values
b = temp[temp['Outcome'] == 0]
m = temp[temp['Outcome'] == 1]
plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク
plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク
plt.xlabel('PC 1') # 第1主成分をx軸
plt.ylabel('PC 2') # 第2主成分をy軸

サポートベクターマシン（SVM）

概要

SVMは未知データに対して与えられた入力データが2つのカテゴリのどちらかに属するかを識別する2値分類モデルである。
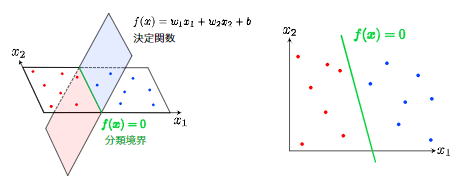
分類境界と呼ばれる境界線をデータ上に示すことで各データ点を分類する。
決定境界とそれに最も近いデータ点であるサポートベクトルの距離をマージンと呼び、これを最大化するのがSVMの目的である。

決定関数と分類境界

• 決定関数f(x)はベクトルxの入力に対してスカラーの値を返す関数
  • wとbは未知のパラメータ
• 決定関数f(x)のパラメータ推定方法は下記の通り
  • 引数が正なら+1
  • 引数が負なら-1

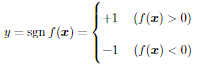
• f(x)=0は分類境界と呼ばれ分けたい2つのクラスを識別するための基準となる
  • サポートベクトル＝分類境界に最も近いデータ
  • マージン最大化＝サポートベクトルを最大にしようとする考え方。SVMではマージン最大化を目的にパラメータの推定を実施

ハードマージンとソフトマージン

• ハードマージン
  • 分離可能性を仮定したサポートベクトル群

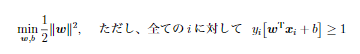
• ソフトマージン
  • ハードマージンを分離可能でないデータに適用できるように拡張したもの
  • ξはデータや誤分類されたデータに対する誤差を表すスラック変数
  • 係数Cは正則化係数呼ばれる学習前に値を与えておく必要があるハイパーパラメータ（正の定数）

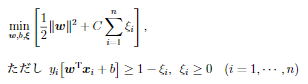
カーネルトリック

特徴ベクトルを非線形変換してその空間での線形分類を行う手法
　例）写像＝高次元へのデータ拡張

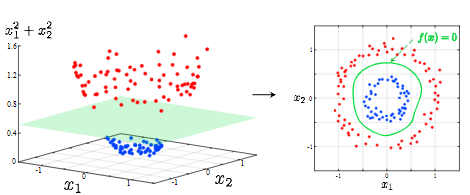
決定関数は下記の通り。代表的な関数形に多項式カーネル、ガウスカーネル、シグモイドカーネルが挙げられる。

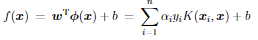
実装（線形SVM）

線形のSVMを実施するにあたりデータを生成。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def gen_data():
    x0 = np.random.normal(size=50).reshape(-1, 2) - 2.
    x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
    X_train = np.concatenate([x0, x1])
    ys_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return X_train, ys_train

X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)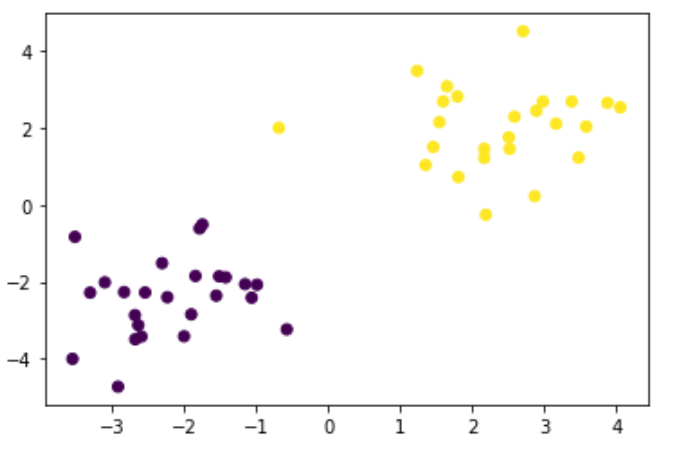

生成したデータに対して線形SVMを実施

t = np.where(ys_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
K = X_train.dot(X_train.T)

eta1 = 0.01
eta2 = 0.001
n_iter = 500

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.where(a > 0, a, 0)

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
    for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
        y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)

plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')

#plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])


plt.quiver(0, 0, 0.1, 0.35, width=0.01, scale=1, color='pink')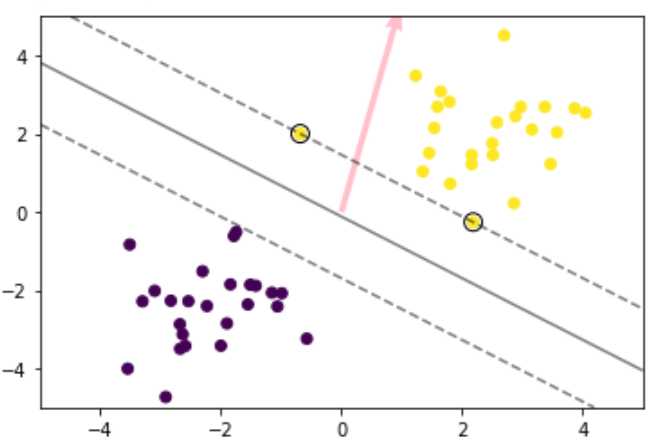

実装（非線形SVM）

非線形のSVMを実施するにあたりデータを生成。

factor = .2
n_samples = 50
linspace = np.linspace(0, 2 * np.pi, n_samples // 2 + 1)[:-1]
outer_circ_x = np.cos(linspace)
outer_circ_y = np.sin(linspace)
inner_circ_x = outer_circ_x * factor
inner_circ_y = outer_circ_y * factor

X = np.vstack((np.append(outer_circ_x, inner_circ_x),
               np.append(outer_circ_y, inner_circ_y))).T
y = np.hstack([np.zeros(n_samples // 2, dtype=np.intp),
               np.ones(n_samples // 2, dtype=np.intp)])
X += np.random.normal(scale=0.15, size=X.shape)
x_train = X
y_train = y

plt.scatter(x_train[:,0], x_train[:,1], c=y_train)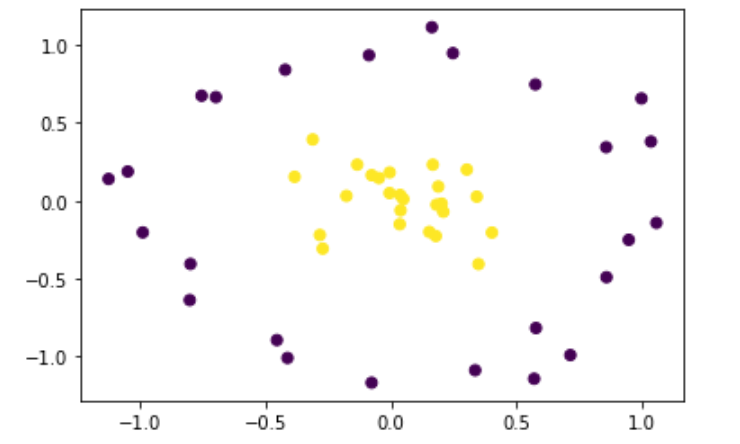

生成したデータに対して非線形SVMを実施

def rbf(u, v):
        sigma = 0.8
        return np.exp(-0.5 * ((u - v)**2).sum() / sigma**2)
    
X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# RBFカーネル
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
    for j in range(n_samples):
        K[i, j] = rbf(X_train[i], X_train[j])

eta1 = 0.01
eta2 = 0.001
n_iter = 5000

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.where(a > 0, a, 0)

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-1.5, 1.5, 100), np.linspace(-1.5, 1.5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
    for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
        y_project[i] += a * sv_t * rbf(X_test[i], sv)
y_pred = np.sign(y_project)

plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])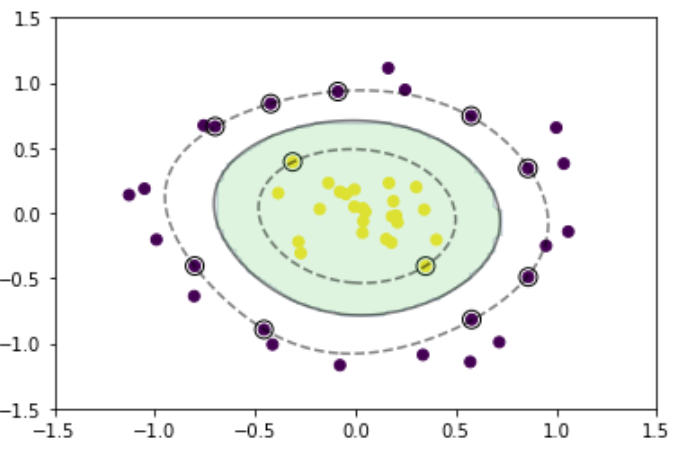

2021/12/26