【E資格】レポートー深層学習（後編）

2021.12.28

この度E資格を受ける前 E資格を受けるために現在ラビットチャレンジを受講中である。その受講内容をレポートとしてまとめる。

今回はRNNからDCGANに至るまでの学んだこと・気づいたことを記す。

再帰型ニューラルネットワークの概念

RNNとは

RNNとは、時系列データに対応可能なニューラルネットワークのことである。
RNNの目的は一定の間隔で時間の特徴がある情報を機会モデルで自律的に獲得させることにある。

時系列データとは、時間的順序を追って一定間隔ごとに観察され，しかも相互に統計的依存関係が認められるようなデータの系列である。
（例：音声データ・株価データ、テキストデータなど）

再帰型ニューラルネットワークでは、時間方向に状態を引き継ぎながら計算を進めることができるため、自然言語や音声などのように、時間方向に順番にならんでいるデータを扱うタスクに向いている。

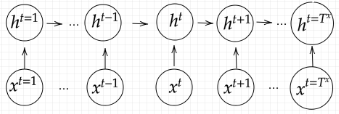
「RNN学習イメージ」という画像内で、「unfold」と記されてる矢印で隔てられている両辺の図は両方ともRNNで実施されている学習イメージを示している。RNNでは中間層に連携された情報を出力層に連携されるだけでなく、再度入力層から連携されたかのように再度中間層に再連携される。
またRNNでは前の中間層から中間層に至るまでの重みも登場する。

RNN学習イメージ

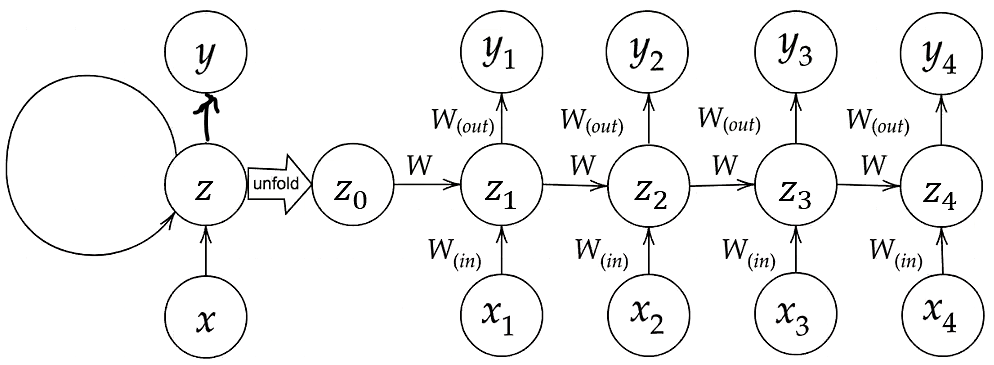
RNNの数式は下記の通り。

$$u^t =W(in)x^t + w_z(t-1)+b$$

u[:,t+1] A= np.dot(X, W_in) + np.dot(z[:,t].reshape(1,-1), W)

$$z^t =f(W(in)x^t + w_z(t-1)+b)$$ 

z[:,t+1] = functions.sigmoid(u[:,t+1])

$$v^t =W(out)z^t + C $$ 

np.dot(z[:,t+1].reshape(1,-1),W_out)

$$y^t =g(W(out)z^t +C)$$ 

z[:,t+1] = functions.sigmoid(u[:,t+1])

RNNで時系列モデルを扱うには、初期の状態と過去の時間t-1の状態を保持し、そこから次の時間でのtを再帰的に求める再帰構造が必要になる。

BPTT

BPTTの正式名称はBack Propagation Through Timeという。RNNにおけるパラメータ調整方法のひとつであり、誤差逆伝播の一種である。

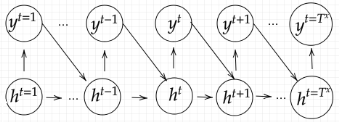
BPTTで実施している全体的な計算は下記の通り。誤差逆伝播法を利用してy^tとd^tに表れた誤差の原因を前の層で修正している。

BPTTにおける誤差関数

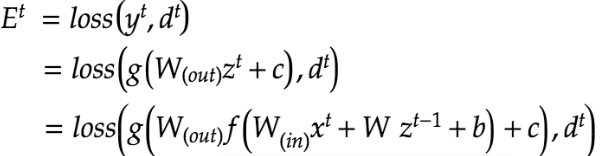
上記の最後の式内の関数gを展開するとz^(t-1)が登場する。また、登場した z^(t-1) を展開すると z^(t-2)が登場し、マトリョーシカのように続く。
この性質によりRNNが再帰的な計算を実現している。

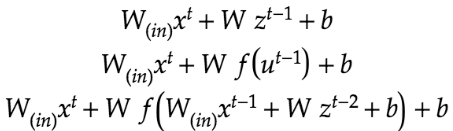
BPTTでは出力層の重みwについて微分による更新を実施。

RNNでBPTTで重みに実施される微分

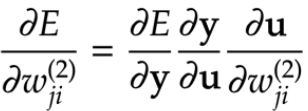
RNNは重みがW(in)、W(Out）、Wの3つについて更新を実施する必要がある。

BPTTにおけるW（in)の更新式
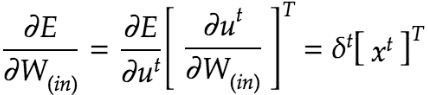
np.dot(X.T,delta[:,t].reshape(1,-1))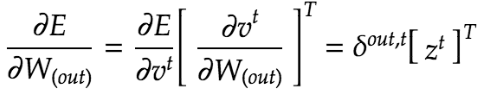
BPTTにおけるW（out)の更新式 
np.dot(z[:,t+1].reshape(1,-1),delta_out[:,t].reshape(1,-1))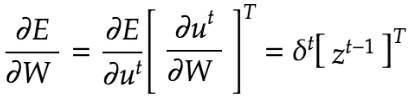
BPTTにおけるWの更新式 
np.dot(z[:,t].reshape(1,-1),delta[:,t].reshape(1,-1))

Tは時間的に遡って微分を実施するという意味である。転置ベクトルの記号Tとは異なることに注意する必要がある。

また、BPTTではバイアスについても下記の通り更新している。右辺に記載されているδ^tはバイアスが更新されている式を集約した記号である。

BPTTにおけるバイアスbの更新式
BPTTにおけるバイアスcの更新式

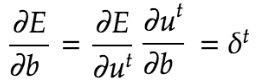
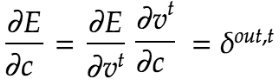
δ^tの詳細な計算方法は下記の通り。

δ^tの計算式「
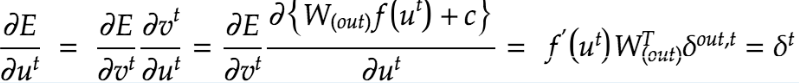
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T))*functions.d_sigmoid(u[:,t])

またBPTTにおけるパラメータの更新は下記の通り。εは学習率を指す。

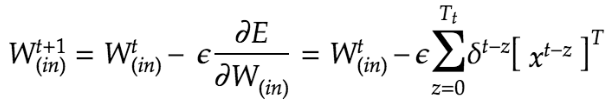
W_in -= learning_rate * W_in_grad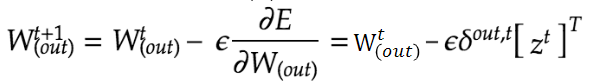
W_out -= learning_rate * W_out_grad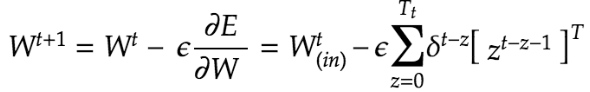
W -= learning_rate * W_grad

実装：RNN

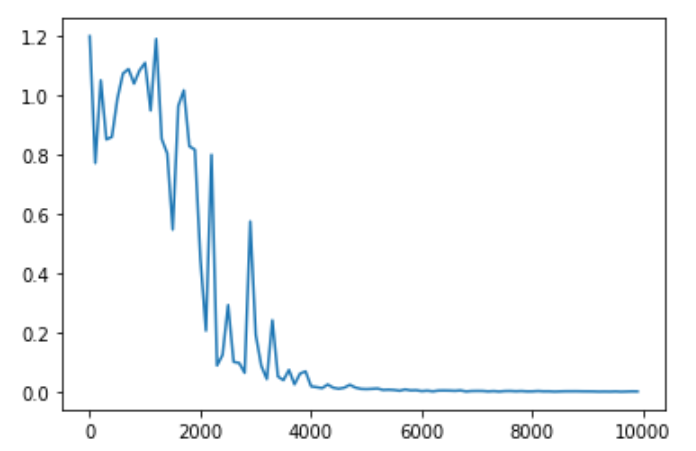
RNNを活用した結果は下記の通り。

import numpy as np
from common import functions
import matplotlib.pyplot as plt


def d_tanh(x):
    return 1/(np.cosh(x) ** 2)

# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)

input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1

weight_init_std = 1
learning_rate = 0.1

iters_num = 10000
plot_interval = 100

# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# Xavier
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size))
# He
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2)
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)


# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))

delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))

all_losses = []

for i in range(iters_num):
    
    # A, B初期化 (a + b = d)
    a_int = np.random.randint(largest_number/2)
    a_bin = binary[a_int] # binary encoding
    b_int = np.random.randint(largest_number/2)
    b_bin = binary[b_int] # binary encoding
    
    # 正解データ
    d_int = a_int + b_int
    d_bin = binary[d_int]
    
    # 出力バイナリ
    out_bin = np.zeros_like(d_bin)
    
    # 時系列全体の誤差
    all_loss = 0    
    
    # 時系列ループ
    for t in range(binary_dim):
        # 入力値
        X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
        # 時刻tにおける正解データ
        dd = np.array([d_bin[binary_dim - t - 1]])
        
        u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
        z[:,t+1] = functions.sigmoid(u[:,t+1])
#         z[:,t+1] = functions.relu(u[:,t+1])
#         z[:,t+1] = np.tanh(u[:,t+1])    
        y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))


        #誤差
        loss = functions.mean_squared_error(dd, y[:,t])
        
        delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])        
        
        all_loss += loss

        out_bin[binary_dim - t - 1] = np.round(y[:,t])
    
    
    for t in range(binary_dim)[::-1]:
        X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

        delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])
#         delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1])
#         delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1])    

        # 勾配更新
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
        W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
        W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
    
    # 勾配適用
    W_in -= learning_rate * W_in_grad
    W_out -= learning_rate * W_out_grad
    W -= learning_rate * W_grad
    
    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0
    

    if(i % plot_interval == 0):
        all_losses.append(all_loss)        
        print("iters:" + str(i))
        print("Loss:" + str(all_loss))
        print("Pred:" + str(out_bin))
        print("True:" + str(d_bin))
        out_int = 0
        for index,x in enumerate(reversed(out_bin)):
            out_int += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
        print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()

出力は下記の通り。

RNNの出力結果

LSTM

RNNは時系列を遡れつれ勾配が消失していくので、長い時系列の学習が課題であった。この解決策として、活性化関数の選択、重みの初期値設定、バッチ正規化でも勾配消失に対応可能であるが、ネットワークの構造自体を変えて解決するアプローチがLSTM（Long Short Term Memory）である。

LSTMはRNNの一種であり、全体図は下記の通り。

LSTMの全体図

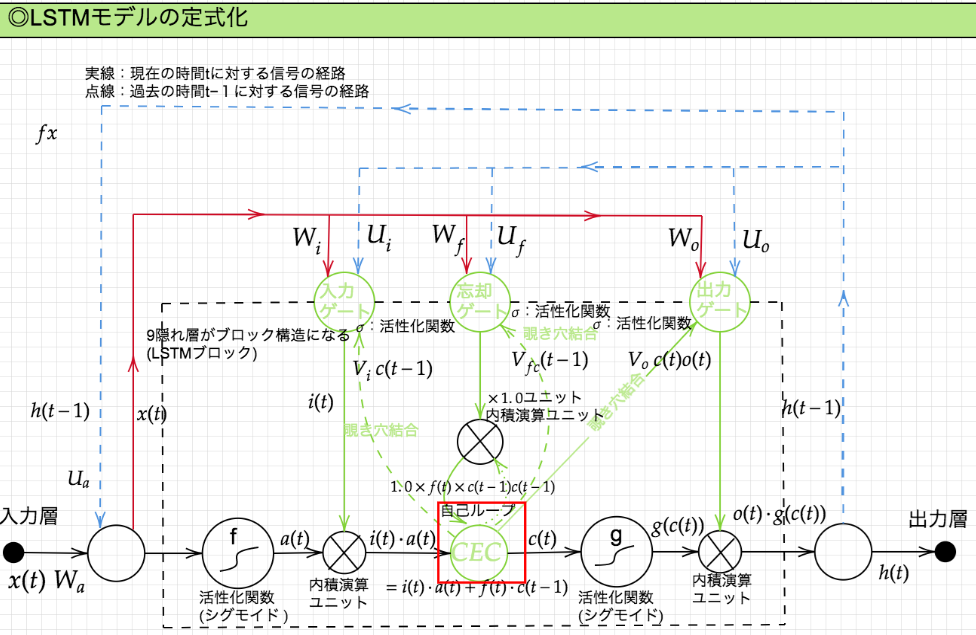
CEC

CEC（Constant Error Carousel）入力値や出力値の記憶機能に特化したモジュールである。スタンダードなRNNでは思考と記憶を同時に行っていたため、時系列を遡るにつれ記憶するが弱まっていた。
したがって、思考機能と記憶機能を分離することで計算が長期化しても記憶性能を維持することに成功した。

CECで行われている処理は下記の通り。

CEC内での処理

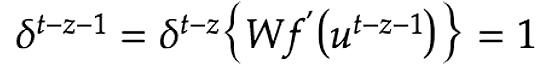
CECは記憶に特化したため、入力データの重みが更新されないためCEC単体ではニューラルネットワークの学習特性が失われている。
したがってCECの周りには学習に必要なモジュールが必要になる。そのモジュールが入力ゲートと出力ゲートとなる。

入力ゲート・出力ゲート

入力ゲートでは内積演算ユニットを通じて連携された入力値を加工してCECに記憶すべきデータを連携する。
出力ゲートではCECが記憶したデータを内積演算ユニットで加工することによって出力値を生成する。
入力ゲート・出力ゲートはともに現在利用中の重みと過去に使用されていた重みの両方を連携されており、時系列を踏まえた適切な加工を実現する。

忘却ゲート

CECは記憶に特化しているため、古すぎる情報でも蓄積してしまい、現在の予測にも古すぎるデータが影響を与えることがある。出力ゲートではどのデータをどれだけ利用するかという処理は行っているが、古すぎる情報を排除するわけではないため、古すぎるデータを予測に利用する可能性が存在する。

その古すぎる情報が予測に利用される可能性を排除するためにLSTMでは忘却でゲートというモジュールが存在する。

覗き穴結合

覗き穴結合とはCEC自身の値に重み行列を介して伝播可能にした構造である。
CECの保存されている過去の情報を任意のタイミングで伝播させたり、忘却させたりすることを実現する。

覗き穴結合はCECが入力ゲート・出力ゲート・忘却ゲートと連結される際に利用されている。

実装

LSTMの実装コードは下記の通り。他のコードや出力結果のデータが膨大になるため本項では実装コードの紹介に留める。

def lstm(x, prev_h, prev_c, W, U, b):
  lstm_in = _activation(x.dot(W.T)) + prev_h.dot(U.T) + b)
  a, i, f, o = np.hsplit(lstm_in, 4)

  a = np.tanh(a)
  input_gate = _sigmoid(i)
  forget_gate = _sigmoid(f)
  output_gate = _sigmoid(o)

  c = input_gate * a + forget_gate * c
  h = output_gate * np.tanh(c)
  return c, h

GRU

スタンダードなLSTMでは、パラメータが多く、計算負荷が高くなることが課題であった。LSTMの計算負荷を低下させたRNNがGRU(Gated recurrent unit)である。

GRUの全体像

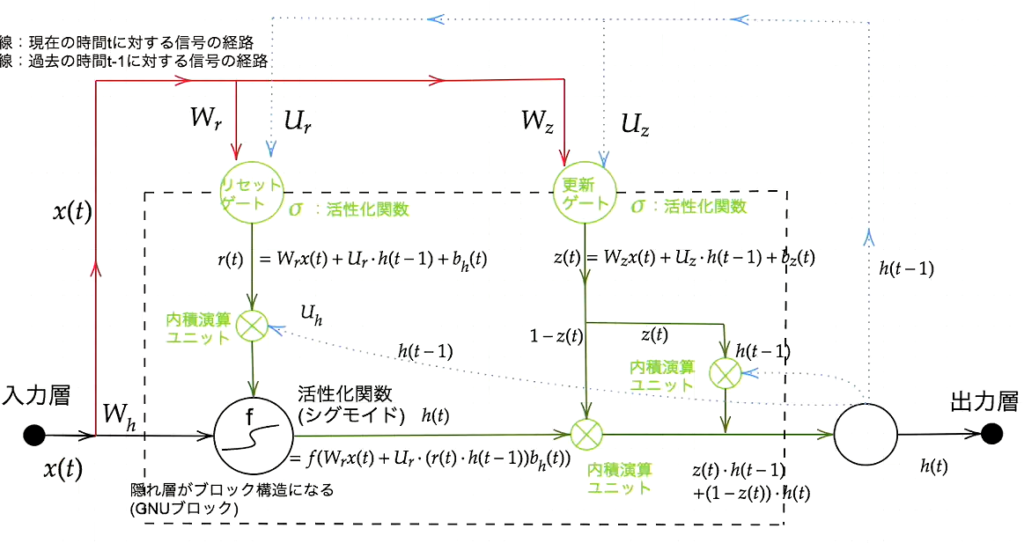
GRUのLSTMとの違いはCEC、入力ゲート、出力ゲート、忘却ゲートが担っていた役割をリセットゲートと更新ゲートというモジュールで代替したいことにある。

GRUはゲート付き回帰型ユニットと呼ばれ、LSTMをシンプルにしたモデルにあり、LSTMより高速に動作する。GRUでは、そのパラメータを大幅に削減し、精度は同等またはそれ以上が望める様になった

実装

GRUの実装コードは下記の通り。他のコードや出力結果のデータが膨大になるため本項では実装コードの紹介に留める。 

def gru(x, h, w_r, U_r, W_z, U_z, W, U):
　　r = _sigmoid(x.dot(w_r, T) + h.dot(U_r.T)
    z = _sigmoid(x.dot(w_z, T) + h.dot(U_z.T)

    h_bar = np.tanh(x.dot(W.T) + (r*h).dot(U.T))
    h_new = (1-z) * h + z * h_bar
    return h_new

双方向RNN

双方向RNNとは時間軸に対して未来方向と過去の方向のRNNを組み合わせたモデルを指す。

双方向性RNNのイメージ

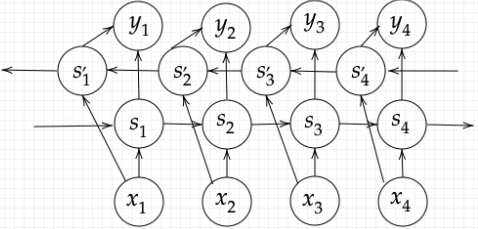
双方向RNNは過去の情報だけでなく、未来の情報を加味することで、精度を向上させている。
(例：文章の推敲、機械翻訳等)

実装

双方向RNNの実装コードは下記の通り。他のコードや出力結果のデータが膨大になるため本項では実装コードの紹介に留める。 

def bidirectional_rnn_net(xs, w_f, U_f, w_b, U\B, V):
    xs_f = np.zeros_like(xs)
    xs_b = np.zeros_like(xs)
    for i, x in enumerate(xs):
        xs_f[i] = x
        xs_b[i] = x[::-1]
    hs_f = _rnn(xs_f, w_f, U_f)
    hs_b = _rnn(xs_f, w_f, U_f)
    hs = [np.concatenate([h_f, h_b[::-1]], axis=1 for h_f, h_b in zip(hs_f, hs_b)]
    ys = hs.dot(V.T)
    return ys

seq2seq

系列(Sequence)を入力として系列を出力する深層学習モデルです。

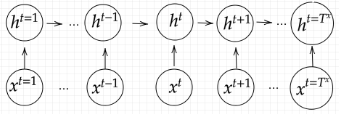
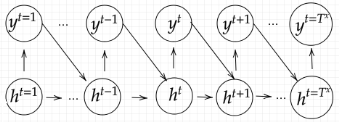
入力系列がEncode(内部状態に変換)され内部状態からDecode(系列に変換)する深層学習モデルである。Encoder-Decoderモデルを採用しており、機械翻訳、機械対話などの文が出力される用途で使用される。

Encoder RNN

Encoder RNNではユーザがインプットしたテキストデータを単語等のトークンに区切って渡す。

Encoder RNN内の処理

Encorder RNNで実施している作業は下記の通り。

  1. Taking: 文章を端強盗のトークンごとに分割し、トークンごとのIDに分割
  2. Embedding: IDから、そのトークンを表す分散表現ベクトルに変換
  3. Encorder RNN:ベクトルを順番にRNNに入力

Encoder RNN内の処理手順は下記の通り。

  1. vec1をRNNに入力し、hidden stateを出力。このhidden stateと次の入力vex2をまたRNNに入力してきたhidden stateを出力という流れを繰り返す
  2. 最後のvecを入れたときのhidden stateをfinal stateとしてとっておく。このfinal stateがthought vectorと呼ばれ、入力した分の意味を表すベクトルとなる

Decoder RNN

Decoder RNNとはシステムがアウトプットデータを単語等のトークン毎に生成する。

Decoder RNN内の処理は下記の通り。

  1. Decorder RNN: Encoder RNNのfinal stateから、各tokenの生成確率を出力するfinal stateをDecorder RNNのinitial stateとして設定し、Embeddingを入力
  2. Sampling: 生成確率に基づいてtokenをランダムに選出
  3. Embedding: Samplingで選ばれたtokenをEmbeddingしてDecoder RNNへの次の入力として設定
  4. Detokenize:1-3を繰り返し、Samplingで獲得したtokenを文字列に変換

HRED

seq2seqでは一問一答のような簡易な会話しか成立できなかったため、より高度なしか対応できなかったのでHREDが開発された。
HREDは過去n-1個の発話から次の発話を生成し、前の単語の流れに即して応答されるため、より人間らしい文章が出力できるようになった。

HREDはseq2seqとContext RNNの側面を併せ持つ。Context RNNはEncoderで集約した各文章の系列を纏めて、これまでの会話コンテキスト全体を表すベクトルに変換する。このContext RNNにより、HREDは過去の発話履歴を加味した返答が可能になった。

HREDの課題は下記の通り。

  • HREDは確率的な多様性が字面にのみあり、会話の「流れ」のような多様性はない。
    • 同じコンテキストを与えられても答えの内容が毎回会話の流れとしては同じものしか出力できない
  • HREDは短く情報量に乏しい答えをしがち
    • 短い頻出される答えを学ぶ傾向（例、うん、そうだね等）

VRED

VREDとはHREDにVAEに潜在変数の概念を追加したモデルである。HREDの課題をVAEの潜在変数の概念を追加することで解決した。

オートエンコーダ

オートエンコーダは教師なし学習の一つ。そのため学習時の入力データは訓練データのみで教師データは利用しない

MNISTでは28×28の数字の画像を入力して同じ画像を出力する際にオートエンコーダを利用

入力データから潜在変数zに変換するニューラルネットワークをEncoderと言い、潜在変数zをインプットとして元画像を復元するニューラルネットワークをDecoderという

オートエンコーダでは次元削減が可能

VAE

オートエンコーダでは潜在変数zの構造が不明

VAEでは潜在変数zに確率分布z~N(0,1)を仮定したもの。 確率分布z~N(0,1) を前提とするこはデータを確率分布の構造に内包することが可能。

実装

seq2seqの内、単語辞書の実装コードは下記の通り。他のコードや出力結果のデータが膨大になるため本項では実装コードの紹介に留める。 

! wget https://www.dropbox.com/s/9narw5x4uizmehh/utils.py
! mkdir images data

# data取得
! wget https://www.dropbox.com/s/o4kyc52a8we25wy/dev.en -P data/
! wget https://www.dropbox.com/s/kdgskm5hzg6znuc/dev.ja -P data/
! wget https://www.dropbox.com/s/gyyx4gohv9v65uh/test.en -P data/
! wget https://www.dropbox.com/s/hotxwbgoe2n013k/test.ja -P data/
! wget https://www.dropbox.com/s/5lsftkmb20ay9e1/train.en -P data/
! wget https://www.dropbox.com/s/ak53qirssci6f1j/train.ja -P data/

import random
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
from nltk import bleu_score

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.nn.utils.rnn import pad_packed_sequence, pack_padded_sequence
from utils import Vocab

# デバイスの設定
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

torch.manual_seed(1)
random_state = 42

def load_data(file_path):
    # テキストファイルからデータを読み込むメソッド
    data = []
    for line in open(file_path, encoding='utf-8'):
        words = line.strip().split()  # スペースで単語を分割
        data.append(words)
    return data

# 訓練データと検証データに分割
train_X, valid_X, train_Y, valid_Y = train_test_split(train_X, train_Y, test_size=0.2, random_state=random_state)

# まず特殊トークンを定義しておく
PAD_TOKEN = '<PAD>'  # バッチ処理の際に、短い系列の末尾を埋めるために使う （Padding）
BOS_TOKEN = '<S>'  # 系列の始まりを表す （Beggining of sentence）
EOS_TOKEN = '</S>'  # 系列の終わりを表す （End of sentence）
UNK_TOKEN = '<UNK>'  # 語彙に存在しない単語を表す （Unknown）
PAD = 0
BOS = 1
EOS = 2
UNK = 3

MIN_COUNT = 2  # 語彙に含める単語の最低出現回数 再提出現回数に満たない単語はUNKに置き換えられる

# 単語をIDに変換する辞書の初期値を設定
word2id = {
    PAD_TOKEN: PAD,
    BOS_TOKEN: BOS,
    EOS_TOKEN: EOS,
    UNK_TOKEN: UNK,
    }

# 単語辞書を作成
vocab_X = Vocab(word2id=word2id)
vocab_Y = Vocab(word2id=word2id)
vocab_X.build_vocab(train_X, min_count=MIN_COUNT)
vocab_Y.build_vocab(train_Y, min_count=MIN_COUNT)

vocab_size_X = len(vocab_X.id2word)
vocab_size_Y = len(vocab_Y.id2word)
print('入力言語の語彙数：', vocab_size_X)
print('出力言語の語彙数：', vocab_size_Y)

出力結果は下記の通り。

入力言語の語彙数： 3725
出力言語の語彙数： 4405

word2vec

word2vecは固定長形式で単語を表すことができるようになった深層学習モデルまたはそのプログラムである。word2vecではone-hotベクトルを利用し、あらゆる単語をベクトルで表現することで固定長形式のデータを作成する子tができるようになった。
RNNでは単語のような可変長の文字列をニューラルネットワークに与えることができなかったRNNの課題をword2vecが解決した。

CBOW

word2vecは正確に言うとCBOW（Continuous Bag-of-Words)モデルとskip-gramの2つのモデルから構成されている。
CBOWモデルコンテキストからターゲットを推測することを目的としており、できるだけ正確な推測ができるように訓練することで、単語の分散表現を獲得することができる。

CBOWモデルのネットワーク

word2vecにより、大規模データの分散表現の学習が現実的な計算速度とメモリ量で実現可能となった。

実装

word2vecの実装は下記の通り。実装コードはオライリージャパン社『ゼロから作るDeep Learningー自然言語処理編』から拝借した。

import sys
sys.path.append('..')
import numpy as np
from common.layers import matmul

    
    text = text.lower() 
    text = text.replace('.', ' .') 
    words = text.split(' ')

    word_to_id = {} 
    id_to_word = {} 

    for word in words: 
        if word not in word_to_id: 
            new_id = len(word_to_id) 
            word_to_id[word] = new_id
            id_to_word[new_id] = word

import sys
sys.path.append('..')
from common.util import preprocess

text = "You are my sunshine."
corpus, word_to_id, id_to_word = preprocess(text)

vocab_size = len(word_to_id)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocan_size)

import sys 
sys.path.append('..')
import numpy as np
from common.layers import MatMul, SoftmaxWithLoss

for create_context_target(corpus, window_size=1)
    target = corpus[window_size:-window_size]
    contexts = []

    for idx in range(window_size, len(corpus)-window_size)
        cs = []
        for t in range(-window_size, windows_size + 1):
            if t == 0:
                 continue
            cs.append(corpus[idx + t])
        return np.array(contexts),np.array(target)

class SimpleCBOW:
  def __init__(self, vocab_size, hidde_size)
      V, H = vocaab_size, hidden_layer_size

      W_in = 0.01 * np.random.randn(V, H).astype('f')
      W_out = 0.01 * np.random.randn(H,.astype('f')

      self.in_layer0 = MatMul(W_in)
      self.in_layer1 = MatMul(W_in)
      self.out_layer = MatMul(W_out)
      self.loss_layer = SoftmaxWithLoss()

      layers = [self.in_layer0, self.in_layer1, self.out_layer]
      self.params, self.grads = [], []
      for layer in layers:
            self.params += layer.params
            self.grads += layer.grads
      
      self.word_vecs = W_in

def forward(self, contexts, target)
    h0 = self.in_layer0.forward(contexts[:,0])
    h1 = self.in_layer0.forward(contexts[:,1])
    h = (h0 +h1) * 0.5
    score = self.out_layer.forward(h)
    loss = self.loss_layer.forward(score, target)
    return loss

def backward(self, dout=1)
    ds = self.loss_layer.backward(dout)
    da = self.out_layer.backward(ds)
    da *= 0.5
    self.in_layer1.backward(da)
    self.in_layer0.backward(da)
    return None

import sys
sys.path.append('..')
from common/trainer import Trainer
from common.optimizer import Adam
from simple_cbow import SimpleCBOW
from common.util import preprocess, create_contexts_target,
    convert_one_hot

window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000

text = 'Your are my sunshine'
corpus, word_to_id, id_to_word =preprocess(text)

vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one?hot(contexts, vocab_size)

model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)

trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()

Attention Mechanism

seq2seq は、固定次元ベクトルの中に入力しなければならないため長い文章への対応しづらいという課題がある。文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていくため、長い文章にも対応できる仕組みが必要である。

Attention Mechanismとは「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組みであり、長い文章に対応するために作成された深層学習モデルである。
翻訳先の各単語を選択する際に、翻訳元の文中の各単語の隠れ状態を利用する。

注意機構イメージ

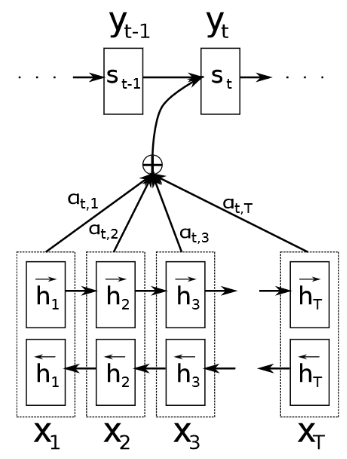
Attention Mechanismでは翻訳元の各単語の隠れ状態の加重平均を用い、重みはFFN（Feed Forward Network）で求める。

翻訳元の各単語の隠れ状態の加重平均の公式
注意機構の重みの公式

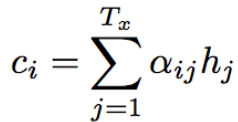
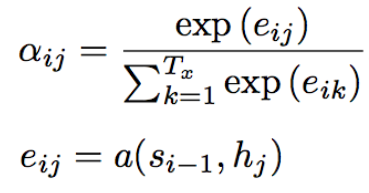
上記の演算を行うことで、queryと呼ばれる検索クエリに一致するKeyを索引し対応するvalueを取り出す操作であると見なす、といった辞書オブジェクトと同等の操作ができるようになった。

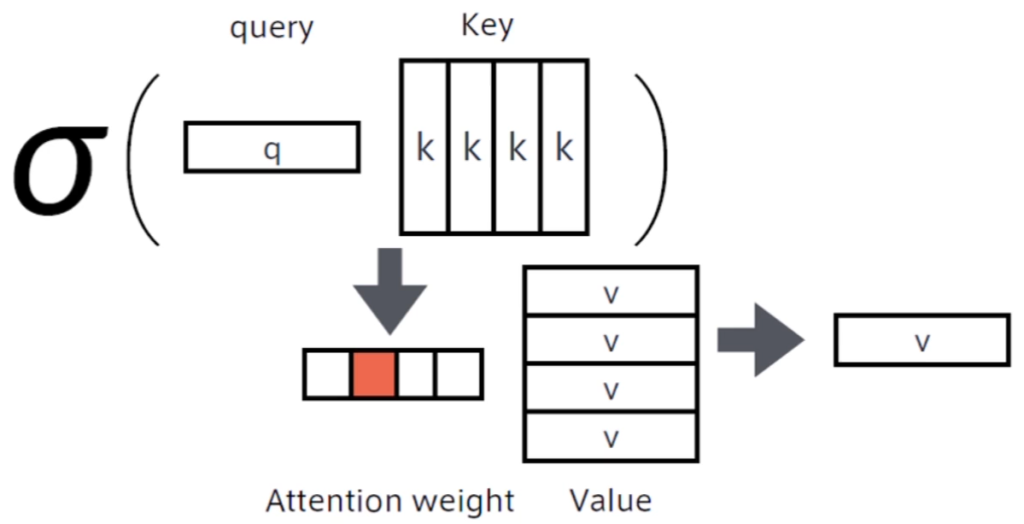
Attention Mechanismが有する自書オブジェクト機能イメージ

強化学習

強化学習とは、長期的に報酬を最大化できるように環境のなかで行動を選択できるエージェントを作ることを目標とする機械学習の一分野を指す。強化学習では行動の結果として与えられる報酬をもとに行動を決定する原理を改善していく。
強化学習は教師なし・あり学習と違い、優れた方策を見つけることが目標である。

学習手法

強化学習はその膨大な計算量により過去には実現することが困難であった。しかし今日ではコンピュータの計算速度の進展と下記のような学習手法により、大規模な強化学習が実現されている。

  • Q学習：行動価値関数を行動するごとに更新することにより学習を進める方法
  • 関数近似法：価値関数や方策関数を関数近似する手法

また、これらの手法に利用されている関数は下記の通り。

  • 価値関数：価値を表す関数としては、状態価値関数と行動価値関数の二種類がある
    • 状態価値関数V^π(s)：強化学習の環境の状態の良し悪しのみで価値が構成されている関数
    • 行動価値関数Q^π(s,a)：状態とエージェントの選択した行動を価値に反映した関数
  • 方策関数π(s)=a：方策ベースの強化学習手法において、ある状態でエージェントがどのような行動をとるのかの確率を与える関数
    • 強化学習ではこの方策を最大化するように学習

AlphaGo

AlphaGoとは強化学習を用いたコンピュータ囲碁ソフトである。強化学習の代表事例として有名なため強化学習の事例として取り上げる。

AlphaGo Lee

PolicyNetは方策関数を用いたAlphaGoである。
囲碁の盤面のデータを何層も畳み込み・プーリングを実施することで、碁盤の各マスの着手予想確率が出力される。

AlphaGo PolicyNet の学習イメージ

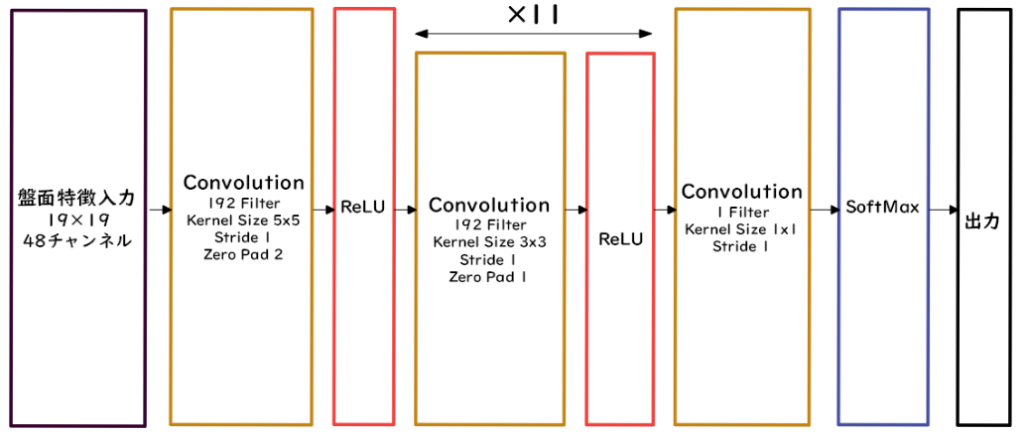
ValueNetでは価値関数を用いたAlphaGoである。
ValueNetでは畳み込み・プーリングを実施後に、全結合層以後で出力を現局面の勝率に置き換えた-1~+1の間で出力される。

AlphaGo ValueNetの学習イメージ


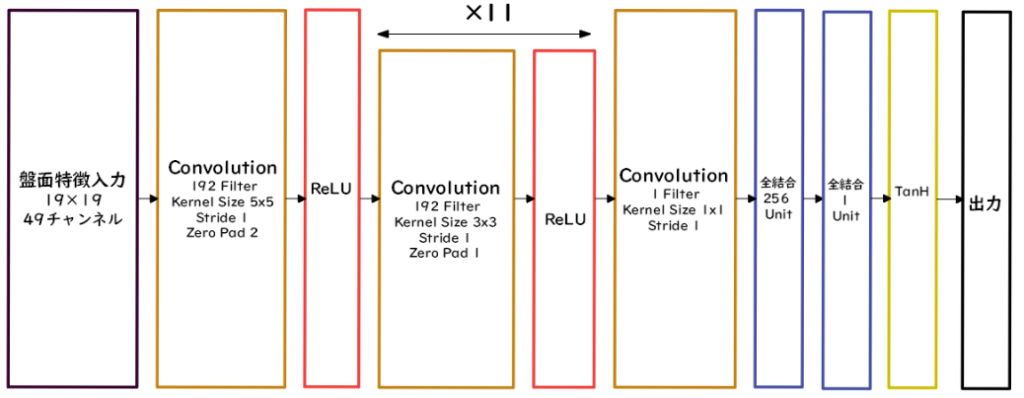
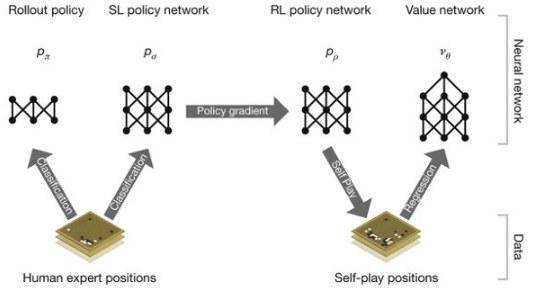
AlphaGo Leeの学習手順は下記の通り

  1. 教師あり学習によるRollOutPolicyとPolicyNetによる学習
  2. 強化学習によるPolicyNetの学習
  3. 強化学習によるValueNetの学習
AlphaGoの処理手順

AlphaGo で利用されている主な技術は下記の通り。

  • RollOutPolicy
    • 線形の方策関数
    • 予測精度は劣るが演算処理が速く、探索中に高速に着手確率を導出するために使用
  • モンテカルロ木探索
    • コンピュータ囲碁ソフトでは現在もっとも有効とされている探索法
    • 盤面の価値や勝率予測値を創出させるために使用

AlphaGo Zero

AlphaGo ZeroとはAlphaGo Leeの後発モデルで、強化学習のみを採用している。

AlphaGo Leeとの違い

  • 教師あり学習を一切行わず、強化学習飲んで作成
  • 特徴入力からヒューリスティックな要素を排除し、碁石の配置のみを入力値に設定
  • PolicyNetとValueNetを1つのネットワークに統合
  • Residual Netを導入
  • モンテカルロ木探索からRollOutシミュレーションを排除

Residual Networkとは勾配爆発・消失を押さえるためにショートカット構造を追加したネットワークのことを指す。

Residual Networkのイメージ
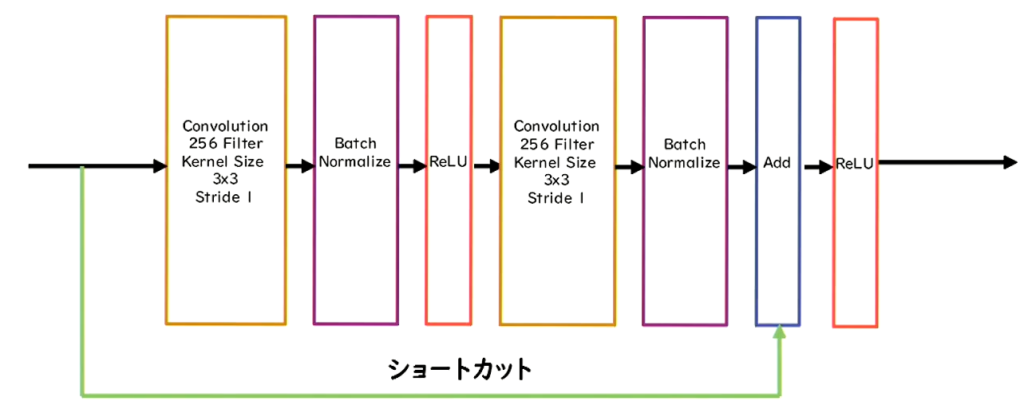
  • 基本構造は
    Convolution⇒BatchNorm⇒ReLU⇒Convolution⇒BatchNorm⇒Add⇒ReLU
    を1ブロックにしている。
  • Residual Networkにより100層を超えるネットワークで安定した学習が可能になった。

軽量化・高速化技術

深層学習は多くのデータを使用したり、パラメータ調整のために多くの時間を使用するため、高速な計算が必要となる。
ムーアの法則に基づくと半導体の集約密度は18～24倍で倍数になるが、深層学習の計算量は1年間で10倍となり、コンピュータの進化速度が深層学習モデルの進化速度に追い付いていない。

上記の背景から、技術者は複数の計算資源を使用し、並列的にニューラルネットを構成することで効率の良い学習を行いたい。そのため、データ並列化、モデル並列化、GPUによる校則技術が不可欠となる。

モデル並列

モデル並列化とは深層学習に活用するコンピュータ（ワーカー）の数を増やし、深層学習用のデータを分割することを指す。

モデル並列化のイメージ

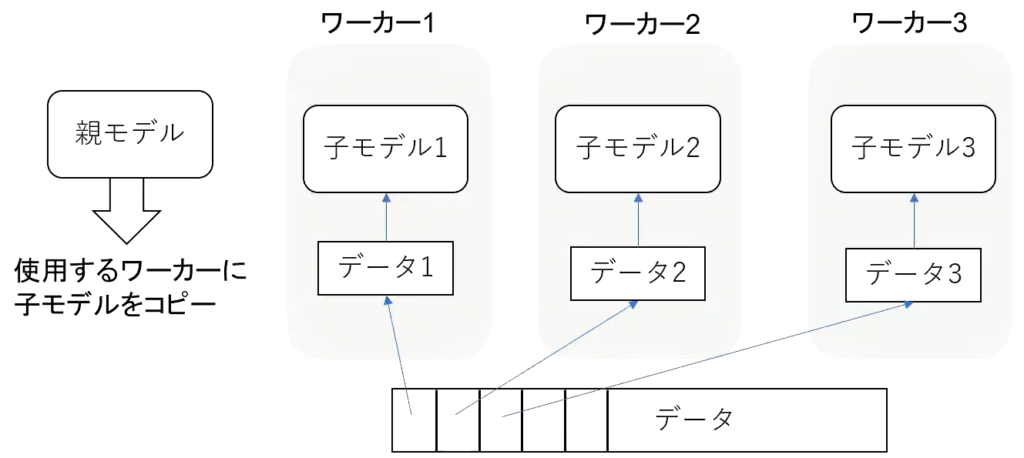
・同期型
同期型のモデル並列化では、各ワーカーが計算が終了するのを待ち、善ワーカーの勾配が出たところで勾配の平均を計算し、親モデルのパラメータを更新する。

同期型モデル並列化のイメージ

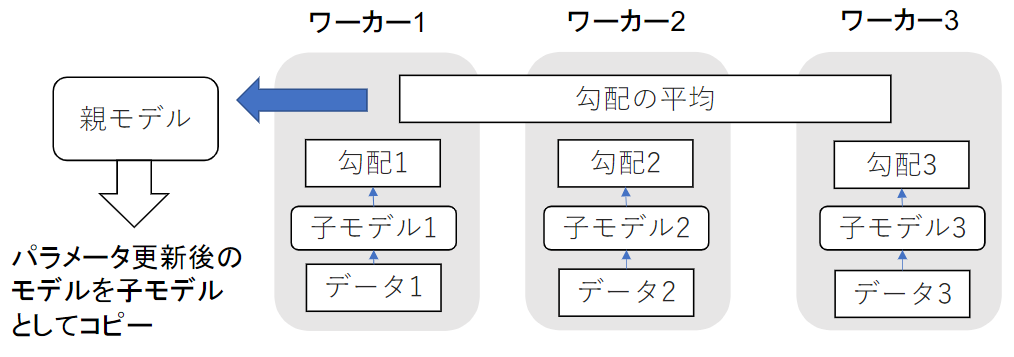
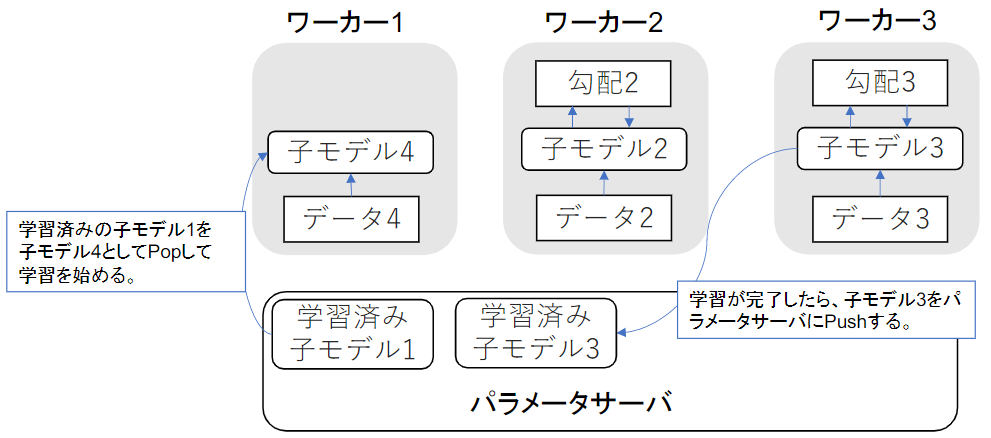
・非同期型
各ワーカーはお互いの計算を待たず、各子モデルごとに更新を実施する。学習が終わった子モデルっはパラメータサーバにPushされる。新たに学習を始めるときは、パラメータサーバからPopしたモデルに対して学習していく。
処理スピードは同期型よりも早いが、最新モデルのパラメータを利用できないので学習が不安定になりやすい。

非同期型モデル並列化のイメージ

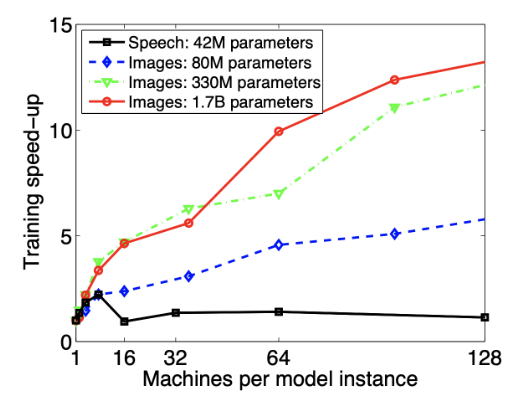
モデル並列化ではモデルのパラメータ数が多くなるにつれ、スピードアップの効率も向上する。

モデルパラメータ数によるモデル並列化のスピードアップ比率

GPU

ワーカーのスペックを向上させることで計算速度を向上させることも可能である。スペック向上に大きく寄与するモジュールがGPUである。
深層学習に利用されるGPUは下記の通り。

  • GPU
    • 比較的低性能なコアが多数
    • 簡単な並列処理が得意
    • ニューラルネットワークの学習は単純な行列演算が多いので高速化が可能
  • GPGPU（General-purpose on GPU）
    • 元々の使用目的であるグラフィック以外の用途で使用されるGPUの総称

主流なGPGPUの開発環境は下記の通り。

  • CUDA
    • GPU上で並列コンピューティングを行うためのプラットフォーム
    • NVIDIA社が開発しているGPUのみで使用可能
    • 深層学習用に提供されているのでユーザビリティが高い
  • OpenCL
    • オープンな並列コンピューティングのプラットフォーム
    • NVIDA社以外の会社（Intel、AMD、RMなど）のGPUからでも使用可能
    • 深層学習用の計算に特化していない

量子化

ネットワークが大きくなると大量のパラメータが必要になり、学習や推論に多くのメモリと演算処理が必要となる。
通常のパラメータの64bit浮動小数点を32bitなど下位の精度に落とすことでメモリと演算処理の削減を行う。

・省メモリ化
ニューロンの重みを浮動小数点のbit数を少なくし有効桁数を下げることでニューロンのメモリサイズを小さくすることができ、多くのメモリを消費するモデルのメモリ使用量を抑えることが可能となる。

省メモリ化のイメージ

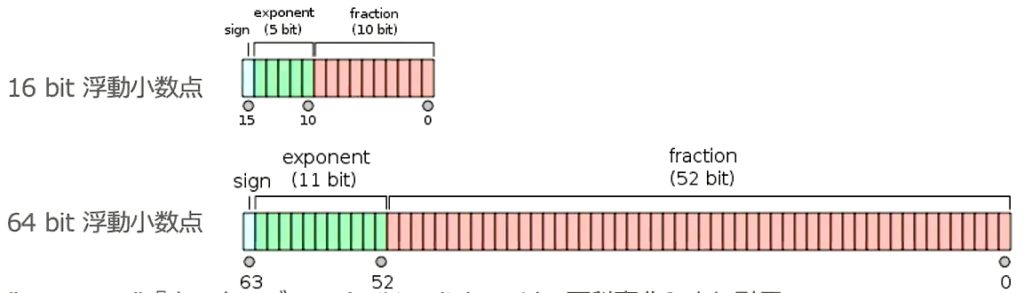
・計算の高速化
64bitと32bitでは演算性能が大きく異なるため、量子化による制度を落とすことによりより多くの計算をすることができる。深層学習で用いられるNVIDA社製のGPUの性能は下記の通り。
64bitから32bitに変更すると約2倍の演算処理となる。

32bit(=単精度演算）64bit(=倍精度演算）
NVIDIA Tesla V100TM15.7 TeraFLOPS7.8 TeraFLOPS
NVIDIA Tesla P00TM 9.3 TeraFLOPS 4.7 TeraFLOPS
量子化による演算処理の影響

省メモリ化をするとニューロンで表現できる少数の有効桁数が小さくなるためモデルの表現力が低下する。しかし、実運用では気にならない程度の表現力の低下になるため量子化は有効な資源節約の手段となる。

蒸留

蒸留とは規模の大きなモデルの知識を軽量なモデル作成に活用することである。蒸留では学習済みの精度の高いモデルの知識を軽量なモデルに継承させる。知識を継承させることで、軽量でありながら複雑なモデルに匹敵する精度のモデルを得ることが期待される。

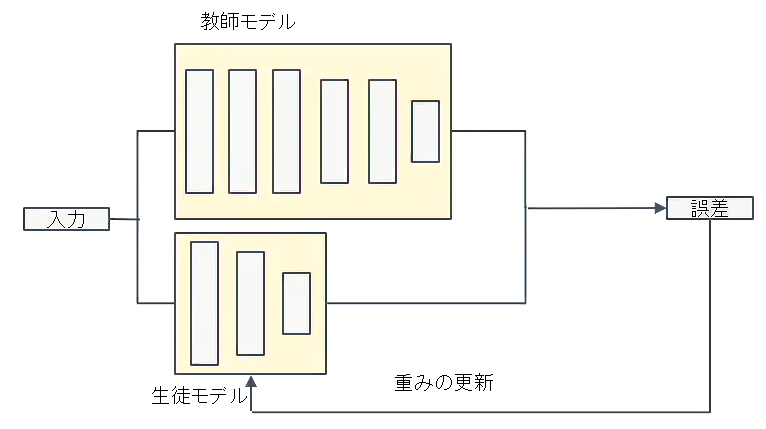
  • 教師モデルと生徒モデル
    教師モデルの重みを固定し生徒モデルの重みを更新していく。誤差は教師モデルと生徒モデルのそれぞれの誤差を使い、重みを更新する。
    • 教師モデル：予測精度の高い、複雑なモデルやアンサンブルされたモデル
    • 子モデル：教師モデルをもとに作成される軽量なモデル
教師モデルと生徒モデルを使用した蒸留

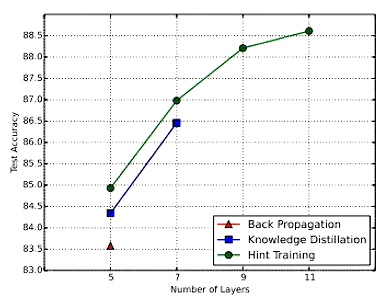
下記グラフ上のback propagation(赤）は通常の学習、Knouledge Distillationは先に説明した蒸留手法、Hint Trainingは引用論文で提案された蒸留手法である。
グラフより上流によって少ない学習回数でより精度の良いモデルを作成することができている。

蒸留による学んだ学習と通常の学習の比較

プルーニング

プルーニングではモデルの制度の寄与が少ないニューロンを削除する。

プルーニングのイメージ

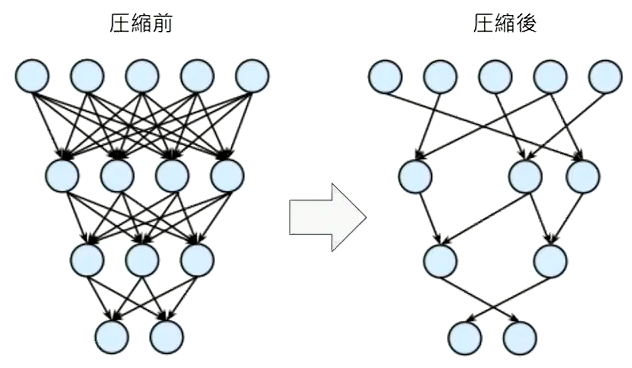
ニューロンの削除の手法は重みが閾値以下の場合のニューロンを削減し、再学習を行う。
プルーニングでは多くのニューロンを削除することができ、学習モデルの予測精度もかなりの割合で維持できることが判明している。

応用モデル

この項では深層学習モデルの具体例として、MobileNet、DenseNet、WaveNetの3つを取り上げる。

MobileNet

  • 画像認識に利用されている認識モデル
  • 一般的な畳み込みレイヤーでは下記のような計算が行われている
    • 入力特徴マップ(チャネル数：H×W×C
    • 畳み込みカーネルのサイズ：K×K×C
    • 出力チャネル数（フィルタ数）：M
    • ストライド1でパディングを適用した場合の畳み込み計算量：H×W×K×K×C×M
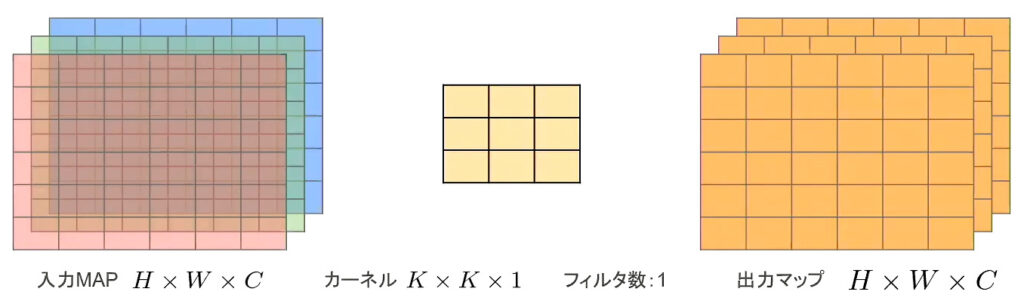
  • MobileNetではDepthwise Convolutionで軽量化をしている
    • 入力特徴マップ(チャネル数：H×W×C
    • 畳み込みカーネルのサイズ：K×K×1
    • 出力チャネル数（フィルタ数）：H×W×C
    • 出力マップの計算量：H×W×K×K×C
Depthwise Convolutionのイメージ
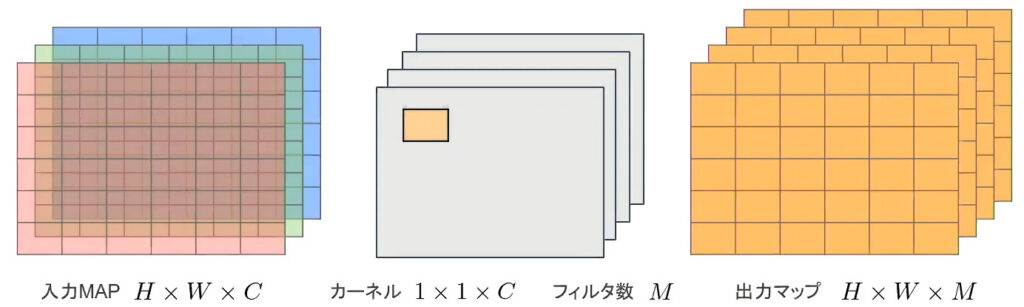
  • MobileNetではPointwise Convolutionで軽量化をしている（入力マップのポイントごとに畳み込み）
    • 入力特徴マップ(チャネル数：H×W×C
    • 畳み込みカーネルのサイズ：K×K×1
    • 出力チャネル数（フィルタ数）：H×W×C
    • 出力マップの計算量：H×W×C×M
Pointwise Convolutionのイメージ

DenseNet

  • 画像認識に利用されている認識モデル
DenseNetの全体イメージ

DenseNetで実施される処理は下記の通り

  1. 層間の情報の伝達を最大にするために全ての同特徴量サイズの層を結合
  2. 特徴マップの入力に対し下記の処理で出力を計算
    • Batch正規化
    • Relu関数による変換
    • 3×3畳み込み層による処理
  3. 中間層でチャネルサイズを変更
  4. 特徴マップのサイズを変更し、ダウンサンプリングを実施
  5. Transition Layerと呼ばれる層が次のDense Blockに連携

WaveNet

  • 音声生成にりようされる深層学習モデル
  • Pixel CNN（高解像度の画像を精密に生成できる深層学習モデル）を音声に応用したもの
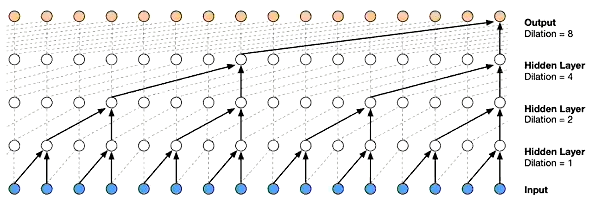
  • 時系列データに対してDilated Convolutionを適用する
    • 層が深くなるにつれて畳み込むリンクを話す
    • 受容野を簡単に増やせることがメリット
Dilated Convolutionのイメージ

Transformer

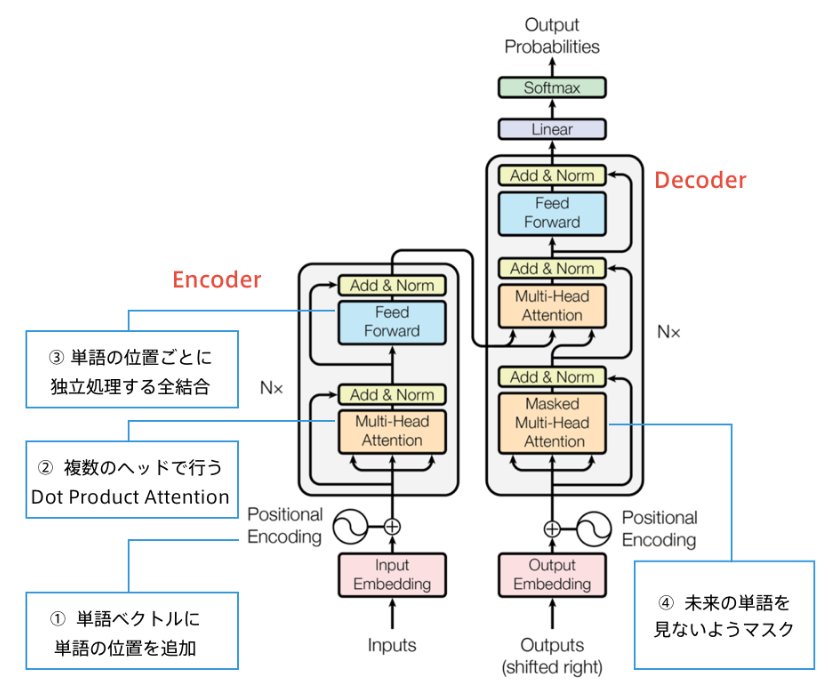
Transformerは2017年6月に発表された、Attention Mechanismを応用した深層学習モデルである。
特徴は下記の通り。

  • Attentionのみで自然言語分野の深層学習を行い、RNNの再帰機能やCNNの畳み込み機能が排除
    • 深層学習で利用する計算量を大幅に削除
    • 2017年当時のSOTAをはるかに少ない計算量で実現し、英仏（3,600万文）の学習を8GPUで3.5日で完了
Transformerイメージ

実装

Transformerは原典のデータを活用し実装する必要がある。
参考実装：https://github.com/jadore801120/attention-is-all-you-need-pytorch

他のコードや出力結果のデータが膨大になるため本項ではPojisition Encodingの実装コードの紹介に留める。
データの事前準備は下記の通り。

! wget https://www.dropbox.com/s/9narw5x4uizmehh/utils.py
! mkdir images data

# data取得
! wget https://www.dropbox.com/s/o4kyc52a8we25wy/dev.en -P data/
! wget https://www.dropbox.com/s/kdgskm5hzg6znuc/dev.ja -P data/
! wget https://www.dropbox.com/s/gyyx4gohv9v65uh/test.en -P data/
! wget https://www.dropbox.com/s/hotxwbgoe2n013k/test.ja -P data/
! wget https://www.dropbox.com/s/5lsftkmb20ay9e1/train.en -P data/
! wget https://www.dropbox.com/s/ak53qirssci6f1j/train.ja -P data/

import time
import numpy as np
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

from nltk import bleu_score

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

from utils import Vocab

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

torch.manual_seed(1)
random_state = 42

PAD = 0
UNK = 1
BOS = 2
EOS = 3

PAD_TOKEN = '<PAD>'
UNK_TOKEN = '<UNK>'
BOS_TOKEN = '<S>'
EOS_TOKEN = '</S>'

def load_data(file_path):
   
    data = []
    for line in open(file_path, encoding='utf-8'):
        words = line.strip().split()  # スペースで単語を分割
        data.append(words)
    return data

train_X = load_data('./data/train.en')
train_Y = load_data('./data/train.ja')

# 訓練データと検証データに分割
train_X, valid_X, train_Y, valid_Y = train_test_split(train_X, train_Y, test_size=0.2, random_state=random_state)

Position Encodingの実装は下記の通り。

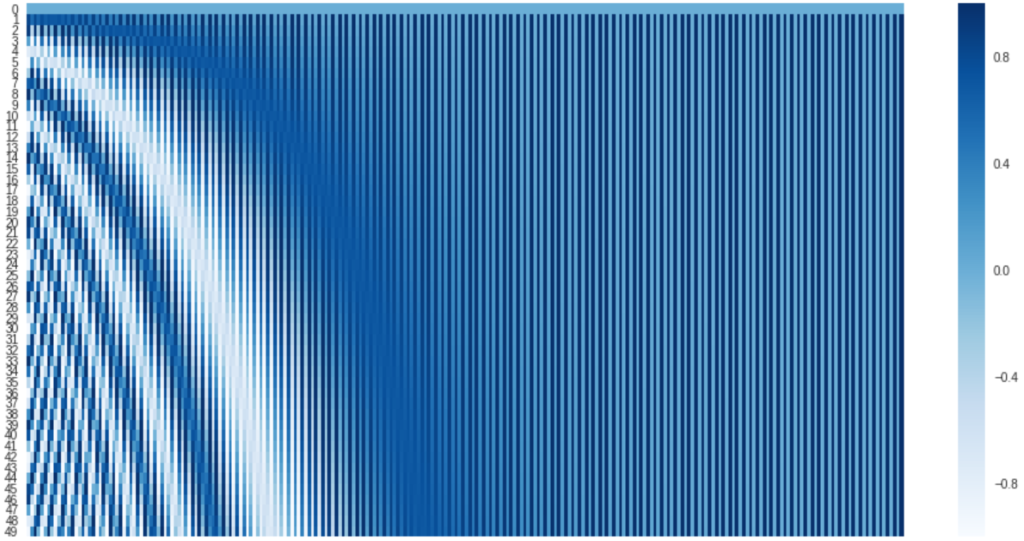
def position_encoding_init(n_position, d_pos_vec):
    """
    Positional Encodingのための行列の初期化を行う
    :param n_position: int, 系列長
    :param d_pos_vec: int, 隠れ層の次元数
    :return torch.tensor, size=(n_position, d_pos_vec)
    """
    # PADがある単語の位置はpos=0にしておき、position_encも0にする
    position_enc = np.array([
        [pos / np.power(10000, 2 * (j // 2) / d_pos_vec) for j in range(d_pos_vec)]
        if pos != 0 else np.zeros(d_pos_vec) for pos in range(n_position)])
    position_enc[1:, 0::2] = np.sin(position_enc[1:, 0::2])  # dim 2i
    position_enc[1:, 1::2] = np.cos(position_enc[1:, 1::2])  # dim 2i+1
    return torch.tensor(position_enc, dtype=torch.float)

pe = position_encoding_init(50, 256).numpy()
plt.figure(figsize=(16,8))
sns.heatmap(pe, cmap='Blues')
plt.show()

出力結果は下記の通り。

Position Encoding部分の出力結果

物体検知・セグメンテーション

タスク名出力備考タスク難易度
分類(Classification)画像に対し単一または複数のクラスレベル物体位置に興味なし易
物体検知
(Object Detection)		Bounding Box [bbox/BB] インスタンスの区別に興味なし中
意味領域分割
(Semantic Segmentation)		各ピクセルに対し単一のクラスレベル インスタンスの区別に興味なし 中
個体領域分割
(Instance Segumentation)		各ピクセルに対し単一のクラスレベル難
物体認識タスクの一覧

データセット

代表的データセットは物体検出コンペティションで用いられるものを使うことが多い。

クラスTrain＋ValidationBox/画像
VOC122011,5402.4
ILSVRC17200476,6681.1
MS COCO1880123,2877.3
OICOD185001,743,0427.0
物体検知用のデータセット

Box/画像はデータの汎用性を示す指標となる。日常生活では物体が溢れており、Box/画像の数値が高いほど日常的なコンテキストで用いられる画像となる。
物体検知の目的によってクラス数やTrain+Validation、Box/画像といった観点でデータセットを選択する必要がある。

評価指標

・IoU：Intersection over Uniion
物体検出においてクラスレベルだけでなく、物体一の予測精度を評価する指標。Jaccard係数とも呼ばれる。

・FPS：Flames per Second
検出精度に加え検出速度も評価する指標。指標を見るときは数値が大きい方がいいのか小さい方が良いのか評価軸の意味を踏まえた上でデータを確認する必要がある。

下記グラフでは1秒あたりに検知できる画像数を記載しているため、横軸は右に行くほど精度の良い物体検知となる。

FPSの事例

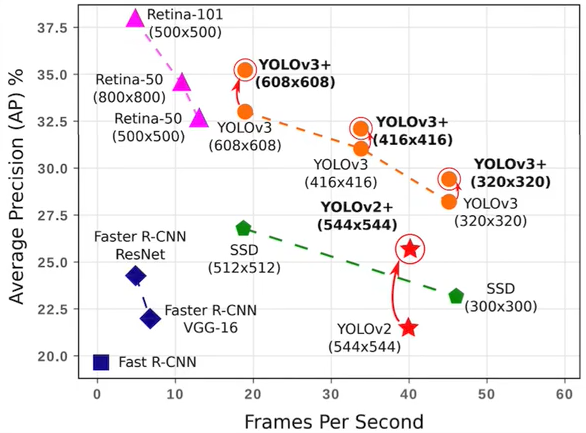
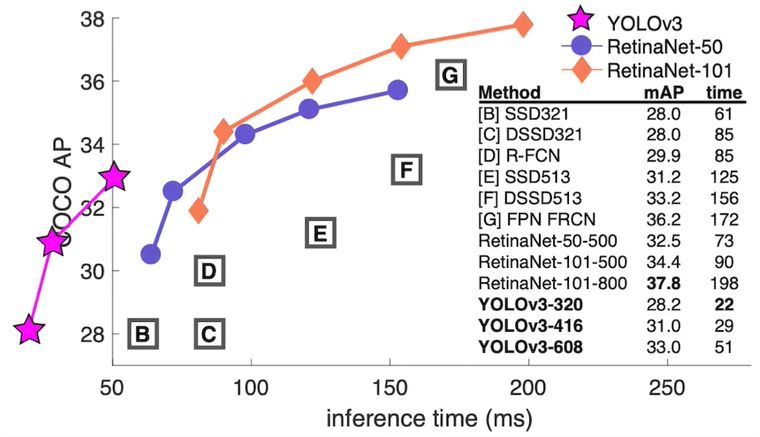
一方次の表では物体検知に要する時間が横軸となっているため、左に行くほど精度の良い物体検知モデルとなる。

Inference Timeの事例

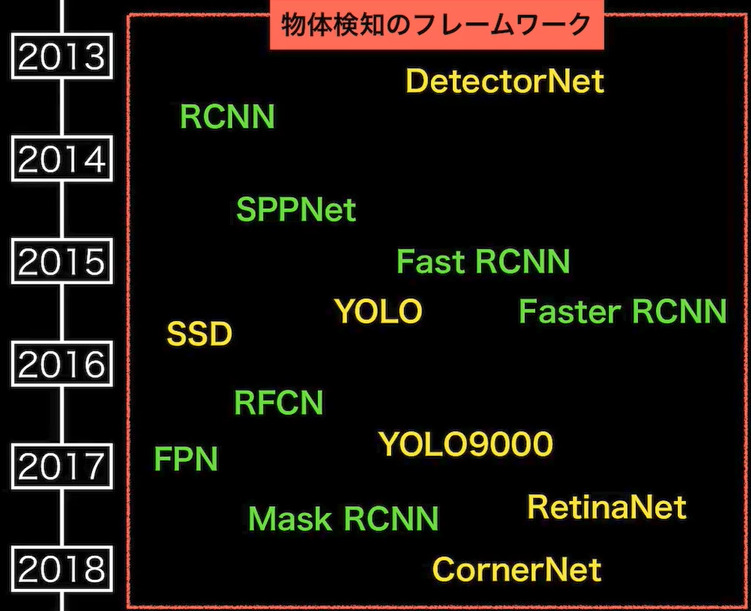
フレームワーク

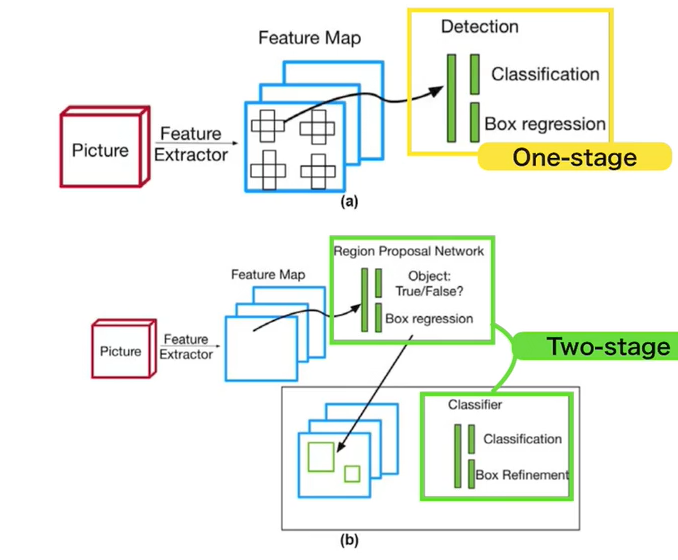
物体検知モデルの名称と登場時期については下記の通り。物体検知モデルの色によって検知タイプが1段階検出器と2段階検出器に分かれる。

物体見地のフレームワークと登場時期
  • 1段階検出器（One-stage detector)
    • 候補領域の検出とクラスの推定を同時に行う
    • 相対的に検知精度が低い
    • 相対的に計算量が小さく推論も早い傾向
  • 2段階検出器（Two-stage detector)
    • 候補領域の検出とクラスの推定を別々に行う
    • 相対的に検知精度が低い
    • 相対的に計算量が大きく推論も遅い傾向
1段階検出器と2段階検出器の手順の違い

SSD（Single Shot Detector)

SSDは代表的な1段階検出器である。VGG16をベースに構成されている。
SSDでは多数のDefalt BOXを用意することによって、物体検知の制度を向上させている。

SDDのイメージ

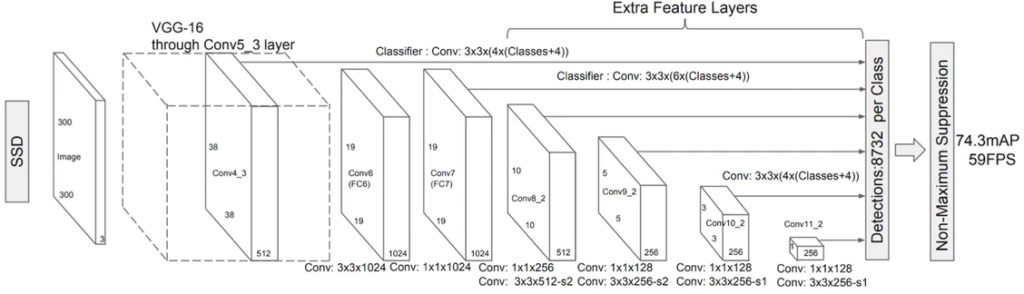
SSDは物体検知の手順は下記の通り。

  1. Default BOXを用意
  2. Default BOXを変形し、conf.を出力

SDDでは多数のDefalt BOXを用意することで2つの問題が生じており、解決策も考案されている。

  1. Non-Maximum Suppression
    1つの物体に対して多数のBounding BOXが用意されている状況に対して、IoUを算出し、IoUが一番大きいBounding BOXを残す。
  2. Hard Negative Mining
    背景として判断されるBounding BOXが非背景に対して過多になってしまう状況に対して、背景と非背景のBounding BOXの比率を規定し、不要な背景を削減する。

DCGAN

GAN

GAN(Genarative Adversarial Nets)は生成器（Generator）と識別器（Discriminator）を競わせて学習する生成＆識別モデルであり、主に画像生成に使用される。

  • Generator：乱数からデータを生成、Genratorに誤認識させようとする
  • Discriminator：入力データが真データ（学習データ）であるかを識別、データを正しく判別しようとする
GANイメージ

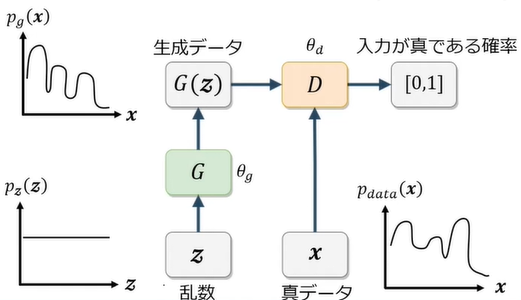
ミニマックスゲーム

GANでは価値関数VがGeneratorとDiscriminatorのミニマックスゲームを行わせるために設定されている。
ミニマックスゲームの概要は下記の通り。

  • プレーヤーAが自分の勝利確率を最大化する作戦を取る
  • プレーヤーBがプレーヤーAの勝利確率を最小化する作戦を取る
GANの価値関数の公式

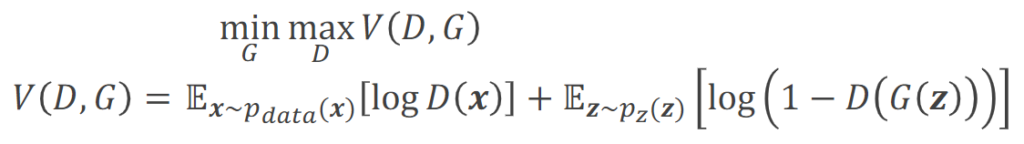
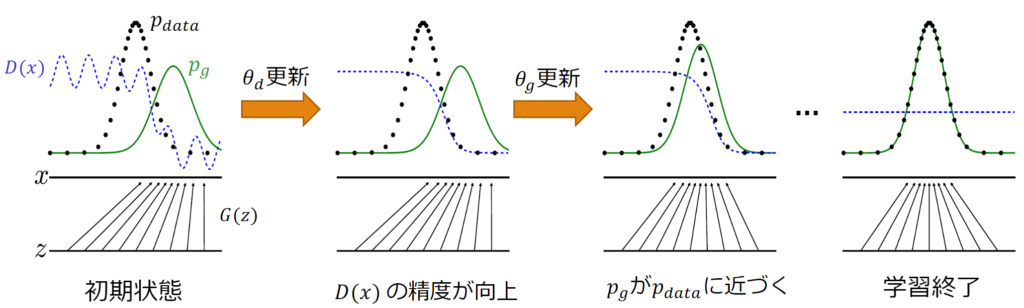
GANは下記のようなステップを経て画像生成を実施する。

GANの学習過程

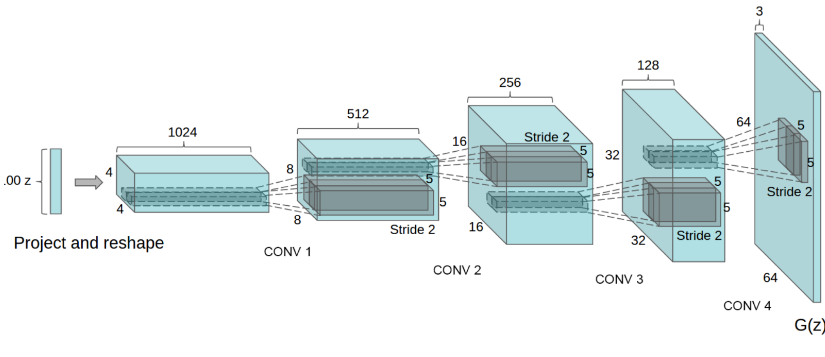
DCGAN

DCGAN（Deep Convolutional GAN）はGANを利用した後継の画像生成の深層学習モデルである。GANに構造制約を加えることで、生成される画像の品質を向上させた。加えられた構造制約は下記の通り。

  • Generator
    • 転置畳み込み層をPooling層に代用（乱数を画像にアップサンプリング）
    • 最終層はtanh、その他はReLU関数で活性化
  • Discriminator
    • 畳み込み層をPooling層に代用（画像から特徴量を抽出し、最終層をigmoid関数で活性化
    • Leaky ReLU関数で活性化
  • 共通事項
    • 中間層に全結合層を排除
    • バッチノーマライゼーションを適用
DCGANのGeneratorイメージ

応用技術

  • Fast Bi-layer Neural Synthesis of One-Shot ealistic Head Avators
    • 1枚の顔画像から動画像（Avator）を高速に生成するモデル
Fast Bi-layer Neural Synthesis of One-Shot Realistic Head Avators生成画像例
  • 構成
    • 初期化：人物の特徴を抽出、1アバターにつき一回の計算コスト
    • 推論：所望の動きをつける、時間フレーム分だけの計算コスト（リアルタイムで実施）
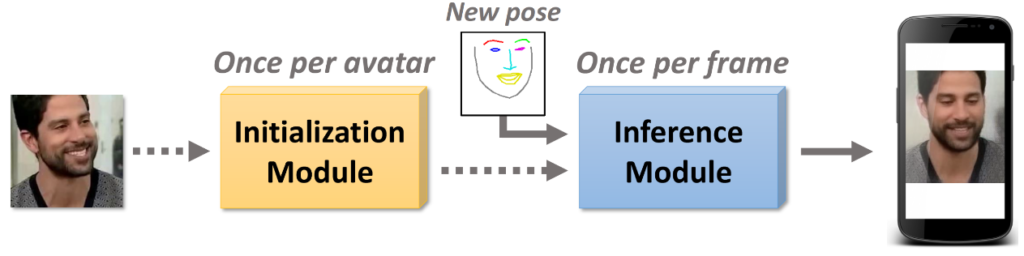
Fast Bi-layer Neural Synthesis of One-Shot Realistic Head Avatorsの処理イメージ

  • 構成
    • 初期化：人物の特徴を抽出、1アバターにつき一回の計算コスト推論：所望の動きをつける、時間フレーム分だけの計算コスト（リアルタイムで実施）

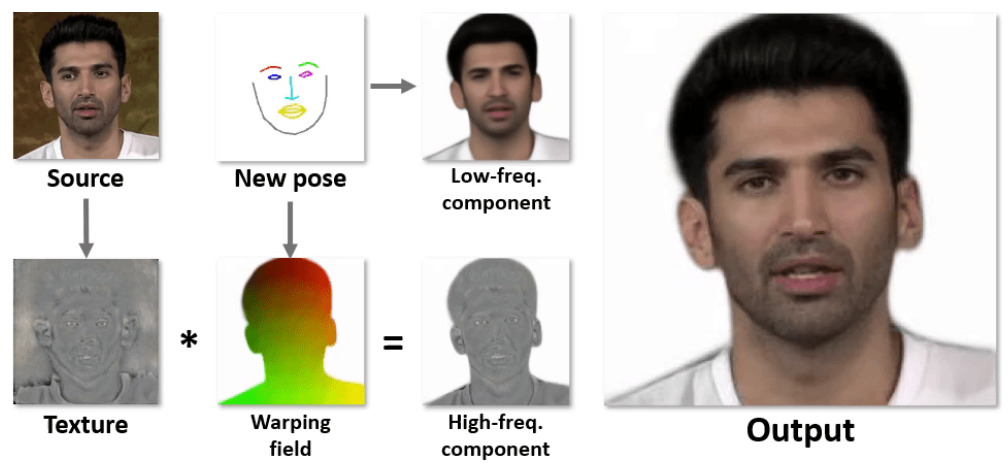
    • 推論部の計算コストの削減方法：
      ⇒緻密な輪郭と粗い顔画像を別々に生成し結合
      • 初期化時に輪郭情報を生成（ポーズから独立）
      • 推論時に粗い動画像を生成（ポーズに依存）
    Fast Bi-layer Neural Synthesis of One-Shot Realistic Head Avatorsの画像生成イメージ

    実装

    GANでDiscriminatorとGeneratorの更新を行うコードは下記の通り。

    def build(self):

    @tf.function
    def update_discriminator(self, noize, real_data):
        fake_data = self.G(noize)

        with tf.GradientTape() as d_tape:
            real_pred = self.D(real_data)
            fake_pred = self.D(fake_data)

            real_loss = tf.keras.losses.binary_crossentropy(tf.ones_like(real_pred), real_pred)
            fake_loss = tf.keras.losses.binary_crossentropy(tf.zeros_like(fake_pred), fake_pred)

            real_loss = tf.math.reduce.mean(real_loss)
            fake_loss = tf.math.reduce.mean(fake_loss)
            adv_loss = real_loss + fake_loss

        d_grad = d_tape.gradient(adv_loss, sources=self.D.trainable_variables)
        self.d_optimizer.apply_gradients(zip(d_grad, self.D.trainable_variables))

    @tf.function

    def update_generator(self, noize):

        with tf.GradientTape() as d_tape:
            real_data = self.G(noize)
            fake_pred = self.D(fake_data)
            fake_loss = -tf.keras.losses.binary_crossentropy(tf.zeros_like(fake_pred), fake_pred)

            fake_loss = tf.math.reduce.mean(fake_loss)
        g_grad = g_tape.gradient(fake_loss, sources=self.G.trainable_variables)
        self.g_optimizer.apply_gradients(zip(g_grad, self.G.trainable_variables))

    コメント

    タイトルとURLをコピーしました